数字图像处理笔记

2 数字图像基础

简单成像模型

\[ f(x,y)=i(x,y)r(x,y) \]

其中$i(x,y)$为入射到被观察场景的光源照射量, $r(x,y)$表示被场景中反射的照射量

\[ 0\le i(x,y)\le \infty \]

\[ 0\le r(x,y)\le1 \]

灰度级数: 表示一个灰度的2的次方数, 比如256, 128等

内插: 把图像放大后中间的像素填充, 邻近内插, 双线性内插, 双三次内插

邻接:

4邻接, 上下左右
8邻接, 上下左右+四对角
m邻接, 优先用4邻接联通, 比如

1 - 1 1 - 1

/ => |

1 1

距离:

$D_4$ 上下左右为1, 斜角为2
$D_8$ 上下左右斜角都为1

仿射变换:

包括缩放,平移,旋转,剪切

变换矩阵:

\[ \large \begin{bmatrix} x' \\ y' \\ 1 \end{bmatrix} = \pmb{A} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} = \begin{bmatrix} a_{11} & a_{12} & a_{13}\\ a_{21} & a_{22} & a_{23}\\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \end{bmatrix} \]

恒等: 矩阵为单位阵

\[ \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

缩放:

\[ \begin{bmatrix} c_x & 0 & 0 \\ 0 & c_y & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

\[ \begin{gather} x'=c_xx \\ y'=c_yy \end{gather} \]

平移:

\[ \begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1 \end{bmatrix} \]

\[ \begin{gather} x'=x+t_x\\ y'=y+t_y \end{gather} \]

垂直剪切:

\[ \begin{bmatrix} 1 & s_v & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

\[ \begin{gather} x'=x+s_vy\\ y'=y \end{gather} \]

水平剪切:

\[ \begin{bmatrix} 1 & 0 & 0 \\ s_h & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \]

\[ \begin{gather} x'=x\\ y'=y+s_hx \end{gather} \]

3 灰度变换与空间滤波

对数变换:

\[ s=c\log(1+r) \]

大部分傅里叶频谱都是这样变换后方便观察

伽马变换:

\[ s=cr^\gamma \]

显示器校正

比特平面分层

直方图均衡: 使得直方图的分布是均匀密度的

直方图匹配(规定化): 使得直方图的分布按照预设的分布分布

性质	卷积	相关
交换律	\(g★f=f★g\)	-
结合律	\(f★(g★h)=(f★g)★h\)	-
分配律	\(f★(g+h)=f★g+f★h\)	\(f☆(g+h)=f☆g+f☆h\)

4 频率域滤波

欧拉公式:

\[ e^{j\theta}=\cos(\theta)+j\sin(\theta) \]

推导: 把$e^\theta$用泰勒公式展开, 然后带入$j$

傅里叶变换:

\[ \Im{\{f(t)\}}=\int^{\infty}_{-\infty}f(t)e^{-j2\pi\mu t}\text{d}t \]

反变换:

\[ f(t)=\int^{\infty}_{-\infty}F(\mu)e^{j2\pi\mu t}\text{d}\mu \]

卷积定理:

\[ \begin{gather} (f★h)(t)\Leftrightarrow(H\cdot F)(\mu)\\ (f\cdot h)(t)\Leftrightarrow(H★F)(\mu) \end{gather} \]

离散傅里叶变换:

\[ \large \begin{gather} F(u)=\sum^{M-1}_{x=0}f(x)e^{-j2\pi ux/M}\\ f(x)=\frac{1}{M}\sum^{M-1}_{u=0}F(u)e^{j2\pi ux/M} \end{gather} \]

二维离散傅里叶变换:

\[ \large \begin{gather} F(u,v)=\sum^{M-1}_{x=0}\sum^{N-1}_{y=0}f(x,y)e^{-j2\pi(ux/M+vy/N)}\\ f(x,y)=\frac{1}{MN}\sum^{M-1}_{u=0}\sum^{N-1}_{v=0}F(u,v)e^{j2\pi(ux/M+vy/N)} \end{gather} \]

平移和旋转:

\[ \large \begin{gather} f(x,y)e^{j2\pi(u_0x/M+v_0x/N)}\Leftrightarrow F(u-u_0,v-v_0)\\ f(x-x_0,y-y_0)\Leftrightarrow F(u,v)e^{-j2\pi(u_0x/M+v_0x/N)} \end{gather} \]

使用极坐标

\[ x=r\cos(\theta),y=r\sin(\theta),u=\omega\cos(\varphi),v=\omega\sin(\varphi) \]

得到:

\[ f(r,\theta+\theta_0)=F(\omega,\varphi+\theta_0) \]

频谱和原图是同方向角度旋转

二维卷积定理:

\[ (f\cdot h)(x,y)\Leftrightarrow \frac{1}{MN}(F★H)(u,v) \]

频域滤波公式:

\[ g(x,y)=\text{Real}\left\{\Im^{-1}[H(u,v)F(u,v)] \right\} \]

要使得频谱中心对称, 原数据得乘以$(-1)^{x+y}$

理想低通滤波器:

存在振铃效应

高斯低通:

\[ \large H(u,v)=e^{-D^2(u,v)/2\sigma^2} \]

没有振铃效应

巴特沃斯低通:

\[ \begin{gather} H(u,v)=\frac{1}{1+\left [D(u,v)/D_0\right]^{2n}}\\ \qquad D(u,v)=\left[(u-P/2)^2+(v-Q/2)^2\right] \end{gather} \]

高通:

\[ H_{\text{HP}}(u,v)=1-H_{\text{LP}}(u,v) \]

高频强调滤波:

\[ g(x,y)=\Im^{-1}\left\{\left[k_1+k_2H_{\text{HP}}(u,v)\right]F(u,v)\right\} \]

同态滤波:

根据照射-反射模型

\[ \begin{gather} f(x,y)=i(x,y)r(x,y)\\ z(x,y)=\ln f(x,y)=\ln i(x,y)+\ln r(x,y) \end{gather} \]

傅里叶变换后频域滤波再反变换

5 图像复原与重建

退化模型:

\[ \begin{gather} g(x,y)=(h\bigstar f)(x,y)+\eta (x,y) \\ G(u,v)=H(u,v)F(u,v)+N(u,v) \end{gather} \]

空间滤波:

算术平均:

\[ \large \hat{f}(x,y)=\frac{1}{mn}\sum_{(r,c)\in S_{xy}}g(r,c) \]

几何平均:

\[ \large \hat{f}(x,y)=\left[\prod_{(r,c)\in S_{xy}}g(r,c)\right]^{\frac{1}{mn}} \]

谐波平均:

\[ \large \hat{f}(x,y)=\frac{mn}{\sum_{(r,c)\in S_{xy}}\frac{1}{g(r,c)}} \]

反谐波平均:

\[ \large \hat{f}(x,y)=\frac{\sum_{(r,c)\in S_{xy}}g(r,c)^{Q+1}}{\sum_{(r,c)\in S_{xy}}g(r,c)^Q} \]

中值滤波:

\[ \large \hat{f}(x,y)=\sideset{}{}{\text{median}}_{(r,c)\in S_{xy}}\{g(r,c)\} \]

最大值:

\[ \large \hat{f}(x,y)=\sideset{}{}{\text{max}}_{(r,c)\in S_{xy}}\{g(r,c)\} \]

最小值:

\[ \large \hat{f}(x,y)=\sideset{}{}{\text{min}}_{(r,c)\in S_{xy}}\{g(r,c)\} \]

中点:

\[ \large \hat{f}(x,y)=\frac{1}{2}\left[\sideset{}{}{\text{max}}_{(r,c)\in S_{xy}}\{g(r,c)\}+\sideset{}{}{\text{min}}_{(r,c)\in S_{xy}}\{g(r,c)\}\right] \]

修正阿尔法均值滤波:

\[ \large \hat{f}(x,y)=\frac{1}{mn-d}\sum_{(r,c)\in S_{xy}}g_R(r,c) \]

自适应滤波器:

自适应局部降噪:

\[ \Large \hat{f}(x,y)=g(x,y)-\frac{\sigma_\eta^2}{\sigma_{S_{xy}}^2}[g(x,y)-\bar{z_{S_{xy}}}] \]

自适应均值滤波:

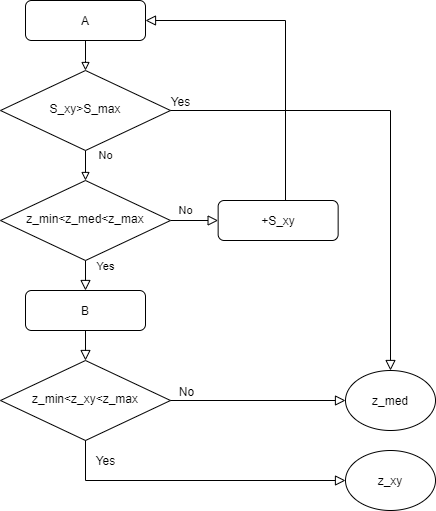
优先保留当前点的值，并且采用更小的窗

运动模糊退化:

$$ \[\begin{gather} g(x,y)=\int^T_0f\left[x-x_0(t),y-y_0(t)\right]\text{d}t\\ G(u,v)=\int^T_0F(u,v)e^{-j2\pi x_0(t)}\text{d}t=F(u,v)\int^T_0e^{-j2\pi [ux_0(t)+vy_0(t)]}\text{d}t\\ H(u,v)=\int^T_0e^{-j2\pi [ux_0(t)+vy_0(t)]}\text{d}t\\ \end{gather}\] $$

令$x_0(t)=at/T$, $y_0(t)=bt/T$

\[ \Large H(u,v)=\frac{T}{\pi(ua+vb)}\sin\left[\pi(ua+vb)\right]e^{-j\pi(ua+vb)} \]

维纳(最小均方差误差)滤波:

对于噪声信号:

\[ x=s+v \]

设计一个滤波器使得y接近原始信号, 即均方误差最小

\[ E\left\{e^2\right\}=E\left\{(s-x\ast h)^2\right\}=\text{min} \]

离散域对h求导:

\[ \begin{align} \frac{\partial\{e^2\}}{\partial h}&=2E\left\{\left[\sum_mh(m)x(n-m)-s(n)\right]\sum_jx(n-j)\right\}\\ &=2E\left\{\sum_mh(m)\sum_jx(n-j)x(n-m)-\sum_js(n)x(n-j)\right\}\\ &=2\sum_mh(m)E\left\{\sum_jx(n-j)x(n-m)\right\}-2E\left\{\sum_js(n)x(n-j)\right\}\\ &=2\sum_mh(m)R_{xx}(j-m)-2R_{xs}(j) \end{align} \]

令导数为0, 得到维纳霍夫方程

\[ R_{xs}(j)=\sum_mh(m)R_{xx}(j-m)\qquad j\ge0 \]

数理统计中:

\[ \begin{gather} R_{xs}=R_{ss}+R_{vs}\\ R_{xx}=R_{ss}+R_{sv}+R_{vs}+R_{vv} \end{gather} \]

s和v互相独立:

\[ \left\{ \begin{matrix} R_{xs}=R_{ss} \\ R_{xx}=R_{ss}+R_{vv} \end{matrix} \right. \]

维纳霍夫方程z变换:

\[ H(z)=\frac{P_{xs}(z)}{P_{xx}(z)}=\frac{P_{ss}(z)}{P_{ss}(z)+P_{vv}(z)} \]

对于FIR系统:

\[ R_{xs}(j)=\sum_{m=0}^{N-1}h(m)R_{xx}(j-m)=\sum_{m=0}^{N-1}h(m)R_{xx}(m-j) \]

获得N个线性方程组:

\[ \begin{align} R_{xs}(0)&=\sum_{m=0}^{N-1}h(m)R_{xx}(m-0)\\ R_{xs}(1)&=\sum_{m=0}^{N-1}h(m)R_{xx}(m-1)\\ ...\\ R_{xs}(N-1)&=\sum_{m=0}^{N-1}h(m)R_{xx}(m-N+1)\\ \end{align} \]

写成矩阵:

\[ \large \begin{bmatrix} R_{xx}(0) & R_{xx}(1) & \cdots & R_{xx}(N-1) \\ R_{xx}(1) & R_{xx}(0) & \cdots & R_{xx}(N-2) \\ \vdots & \vdots & \ddots & \vdots \\ R_{xx}(N-1) & R_{xx}(N-2) & \cdots & R_{xx}(0) \end{bmatrix} \begin{bmatrix} h(0)\\ h(1)\\ \vdots\\ h(N-1) \end{bmatrix} = \begin{bmatrix} R_{xs}(0)\\ R_{xs}(1)\\ \vdots\\ R_{xs}(N-1)\\ \end{bmatrix} \]

简写成:

\[ \mathbb{R}_{xx}\mathcal{H}=\mathbb{R}_{xs} \]

对于非因果系统:

\[ R_{xs}(j)=\sum_{m=-\infty}^{+\infty}h(m)R_{xx}(j-m) \]

变换到$\mathbf{Z}$域:

\[ H(z)=\frac{P_{xs}(z)}{P_{xx}(z)} \]

得到:

\[ h(n)=\frac{1}{2\pi j}\oint H(z)z^{n-1}\text{d}z \]

要得到期望信号才能求解方程, 对于图像来说, 选取参考意义较大的一部分即可

6 彩色图像处理

光的三原色: 红(575nm), 绿(535nm), 蓝(445nm)

CRT显示器: 电子敏感荧光粉

LCD: 偏振光阻止或让光通过

CIE色度图:

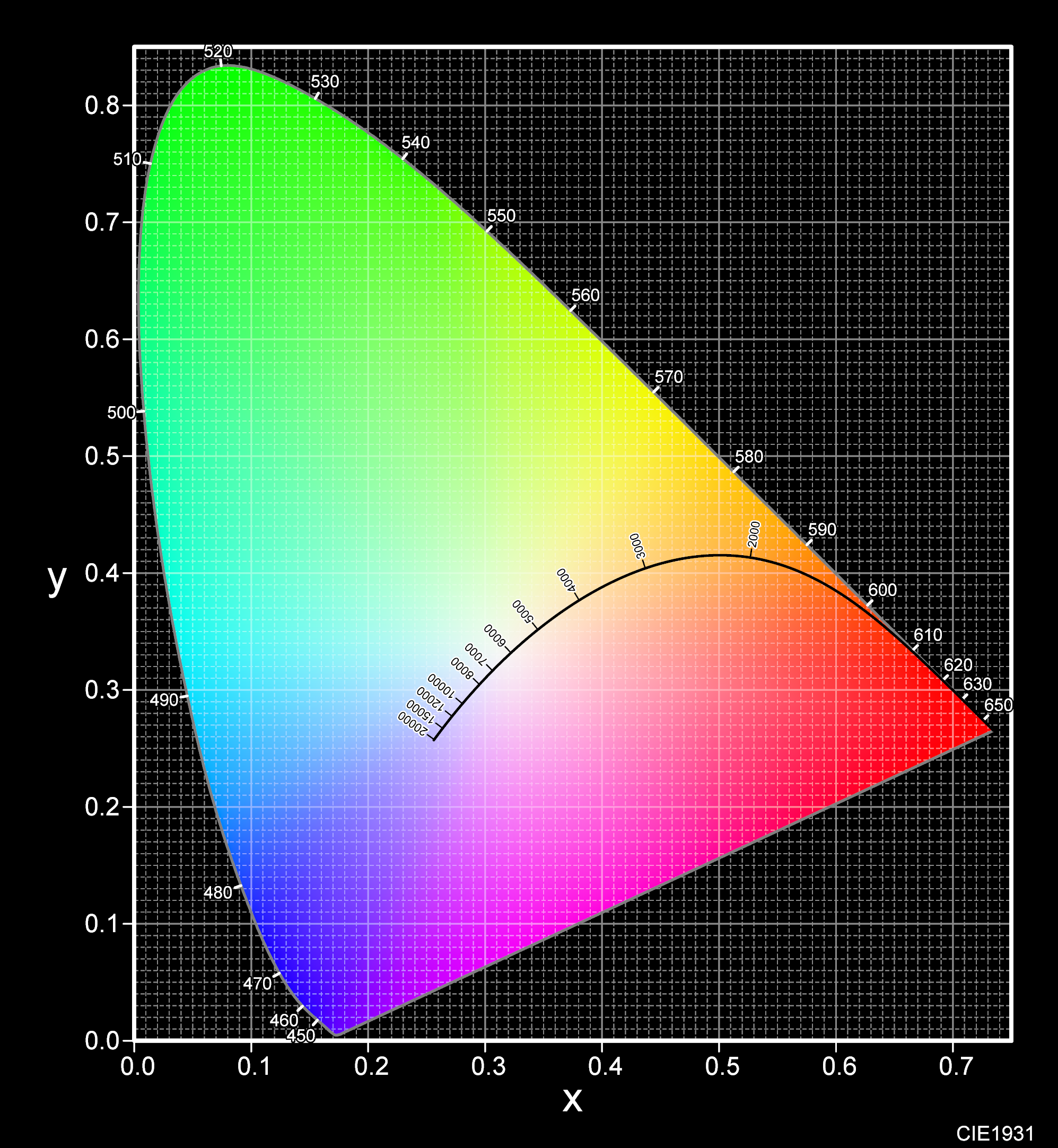
红色, 绿色和蓝色能量用X,Y,Z表示, 三色系数为

\[ \begin{gather} x=\frac{X}{X+Y+Z}\\ y=\frac{Y}{X+Y+Z}\\ z=\frac{Z}{X+Y+Z}\\ z=1-x-y \end{gather} \]

彩色模型的x轴代表x, y轴代表y, 所以在x,y=1/3的地方为白色, 最外圈代表不同波长的光, 从白光到边界上的直线定义该光谱下的所有色度

彩色模型:

RGB, 彩色摄像机
CMY(青色,深红色,黄色), CMYK(青色, 深红色, 黄色, 黑色), 彩色打印机

\[ \begin{gather} CMY=1-RGB\\ CMY\Rightarrow CMYK \left\{\begin{matrix} K=\min(C,M,Y)\\ C=(C-K)/(1-K)\\ M=(M-K)/(1-K)\\ Y=(Y-K)/(1-K) \end{matrix}\right.\\ CMYK\Rightarrow CMY \left\{\begin{matrix} C=C(1-K)/+K\\ M=M(1-K)/+K\\ Y=Y(1-K)/+K \end{matrix}\right. \end{gather} \]

HSI(色调, 饱和度, 亮度), 解释颜色, 解除颜色信息和灰度级的关系

RGB=>HSI

\[ \begin{gather} H=\left\{\begin{matrix} \theta, & B\le G\\ 360-\theta, & B>G \end{matrix}\right.\\ \theta=\arccos\left\{\frac{1/2\left[(R-G)+(R-B)\right]}{\left[(R-G)^2+(R-B)(G-B)\right]^{1/2}}\right\}\\ S=1-\frac{3}{R+G+B}[\min(R,G,B)]\\ I=\frac{1}{3}(R+G+B) \end{gather} \]

HSI=>RGB

\[ \begin{gather} H'=\left\{\begin{matrix} H, & 0°\le H<120°\\ H-120, & 120°\le H<240°\\ H-240, & 240°\le H<360° \end{matrix}\right.\\ I(1-S)=\left\{\begin{matrix} B, & 0°\le H<120°\\ R, & 120°\le H<240°\\ G, & 240°\le H<360° \end{matrix}\right.\\ I\left[1+\frac{S\cos H'}{\cos(60°-H')}\right]=\left\{\begin{matrix} R, & 0°\le H<120°\\ G, & 120°\le H<240°\\ B, & 240°\le H<360° \end{matrix}\right.\\ 3I-(G+B)=\left\{\begin{matrix} G, & 0°\le H<120°\\ B, & 120°\le H<240°\\ R, & 240°\le H<360° \end{matrix}\right.\\ \end{gather} \]

假彩色图: ColorMap

7 小波变换和其他图像变换

对于向量集$\pmb{w}$

\[ \langle\pmb{w}_k,\pmb{w}_l\rangle=0,\qquad k\ne l \]

此时$\pmb{w}$为正交基

对于另一个对偶向量集$\pmb{\tilde{w}}$, 有

\[ \langle\pmb{\tilde{w}}_k,\pmb{w}_l\rangle=0,\qquad k\ne l \]

此时他们为双规范正交基

双规范正交, 对于两个

对于离散的傅里叶变换:

\[ \begin{gather} T(u)=\sum_{x=0}^{N-1}f(x)r(x,u)\\ f(x)=\sum_{u=0}^{N-1}T(u)s(x,u) \end{gather} \]

$r(x,u)$为正变换核, $s(x,u)$为反变换核

用内积表示为:

\[ T(u)=\langle s(x,u),f(x)\rangle \]

对于变换矩阵(实数基):

\[ \pmb{A}\pmb{A}^T=\pmb{I} \]

二维变换:

\[ \large \begin{gather} T(u,v)=\sum_{x=0}^{N-1}\sum_{y=0}^{N-1}f(x,y)r(x,y,u,v)\\ f(x,y)=\sum_{u=0}^{N-1}\sum_{v=0}^{N-1}T(u,v)s(x,y,u,v)\\ r(x,y,u,v)=r_1(x,u)r_2(y,v)\\ \text{xy对称}\qquad r(x,y,u,v)=r_1(x,u)r_1(y,v) \end{gather} \]

则:

\[ \begin{gather} \pmb{T}=\pmb{A}\pmb{F}\pmb{A}^T\\ \pmb{F}=\pmb{A}^T\pmb{T}\pmb{A} \end{gather} \]

把二维变换分解成两个一维变换

对于矩形阵列, 变为:

\[ \begin{gather} \pmb{T}=\pmb{A}_M\pmb{F}\pmb{A}_N^T\\ \pmb{F}=\pmb{A}_M^T\pmb{T}\pmb{A}_N\\ \end{gather} \]

$\pmb{F},\pmb{A}_M,\pmb{A}_N$分别为$M\times N,M\times M,N\times N$

对于复数基:

\[ \begin{gather} \pmb{T}=\pmb{A}\pmb{F}\pmb{A}^T\\ \pmb{F}=\pmb{A}^{*T}\pmb{T}\pmb{A}^*\\ \pmb{A}^{*T}\pmb{A}=\pmb{A}\pmb{A}^{*T}=\pmb{A}^*\pmb{A}^T=\pmb{A}^T\pmb{A}^* \end{gather} \]

常见的小波变换有: DHT(离散哈特利), DCT(离散余弦), DST(离散正弦), WHT(沃尔什-哈达玛基), SLT(斜坡基), HAAR(哈尔基), DB4(Daubechies基), BIOR3.1(双正交B样条基)

海森堡不等式:

\[ \sigma^2_t\sigma^2_f\ge\frac{1}{16\pi^2} \]

对于矩形的变换对象:

\[ \begin{gather} f(x,y)=\pmb{F}=\sum_{u=0}^{N-1}\sum_{v=0}^{N-1}T(u,v)S_{u,v} \end{gather} \]

其中$S_{u,v}$为

\[ \large S_{u,v}=\begin{bmatrix} s(0,0,u,v)&s(0,1,u,v)&\cdots&s(0,N,u,v)\\ s(1,0,u,v)&s(1,1,u,v)&\cdots&s(1,N,u,v)\\ \vdots&\vdots&\ddots&\vdots\\ s(N,0,u,v)&s(N,1,u,v)&\cdots&s(N,N,u,v) \end{bmatrix} \]

可以看作$F$由$N\times N$个$N^2$的矩阵线性组合而成, 如果u,v可分离

\[ S_{u,v}=s_us_v \]

那么$F$为图像, $S_{u,v}$为基图像

离散哈特利变换(DHT):

\[ s(x,y,u,v)=\left[\frac{1}{\sqrt{N}}cas\left(\frac{2\pi ux}{N}\right)\right] \left[\frac{1}{\sqrt{N}}cas\left(\frac{2\pi vy}{N}\right)\right] \]

其中$\text{cas}(\theta)=\cos(\theta)+\sin(\theta)$

离散余弦变换(DCT):

\[ s(x,y,u,v)=\cos\left(\frac{(2x+1)u\pi}{2N}\right)\cos\left(\frac{(2y+1)v\pi}{2N}\right) \]

离散正弦变换(DST):

\[ s(x,y,u,v)=\frac{2}{N+1}\sin\left(\frac{(x+1)(u+1)\pi}{N+1}\right) \sin\left(\frac{(y+1)(v+1)\pi}{N+1}\right) \]

沃尔什-哈达玛变换(WHT):

\[ \LARGE s(x,y,u,v)=\frac{1}{N}(-1)^{\sum_{i=0}^{n-1}\left[b_i(x)p_i(u)+b_i(y)p_i(v)\right]} \]

其中$b_z(k)$表示z的二进制的第k位, 即(z & (0x1 << k)) >> k

斜变换(SLT)

递归生成

哈尔变换(HAAR):

哈尔函数:

对于任意一个$x\in[0,1)$

\[ \large \begin{gather} u=2^p+q\qquad u>0\\ q=2^p-u\\ h_u(x)=\left\{ \begin{matrix} 1,&u=0,0\le x<1\\ 2^{p/2},&u>0,q/2^p\le x<(q+0.5)/2^p\\ -2^{p/2},&u<0,(q+0.5)/2^p\le x<(q+1)/2^p\\ 0,&other \end{matrix} \right. \end{gather} \]

\[ s(x,u)=\frac{1}{\sqrt{N}}h_u(x/N), \qquad x=0,1,\cdots,N-1 \]

变换矩阵为:

\[ \large H_N=\begin{bmatrix} h_0(0/N)&h_0(1/N)&\cdots&h_0(N-1/N)\\ h_1(0/N)&h_1(1/N)&\cdots&h_1(N-1/N)\\ \vdots&\vdots&\ddots&\vdots\\ h_{N-1}(0/N)&h_{N-1}(1/N)&\cdots&h_{N-1}(N-1/N)\\ \end{bmatrix} \]

小波变换:

尺度函数:

\[ \begin{gather} \{\varphi_{j,k}|j,k\in Z\}\\ \varphi_{j,k}(x)=2^{j/2}\varphi(2^jx-k) \end{gather} \]

$k$决定x轴位置,j决定尺度形状, $V_{j_0}$的基为$j=j_0,k=\cdots,-1,0,1,2,\cdots$

对于哈尔函数

\[ \varphi(x)=\left\{ \begin{matrix} 1,&0\le x<1\\ 0,&other \end{matrix}\right. \]

$V_1$基为$V_0$基的线性组合

\[ \varphi_{0,k}=\frac{1}{\sqrt{2}}\varphi_{1,2k}+\frac{1}{\sqrt{2}}\varphi_{1,2k+1} \]

多分辨率分析的要求:

尺度函数相对于其整数平移是正交的
尺度函数以低尺度张成的函数空间嵌套在高尺度张成的函数空间中, 即

\[ V_{-\infty}\subset\cdots\subset V_{-1}\subset V_0\subset V_1\subset V_2\subset\cdots\subset V_{\infty} \]

在每个尺度上唯一可表示的函数是$f(x)=0$
所有可度量的, 平方可积的函数都可表示为尺度函数在$j\rightarrow\infty$时的线性组合, 即

\[ V_{\infty}=L^2(R) \]

$\varphi(x)$可以表示为自身2倍分辨率的线性组合, 细化膨胀方程

\[ \varphi(x)=\sum_{k\in Z}h_{\varphi}(k)\sqrt{2}\varphi(2x-k) \]

对于规范正交尺度函数, (内积):

\[ h_{\varphi}(k)=\left\langle\varphi(x),\sqrt{2}\varphi(2x-k)\right\rangle \]

小波函数:

递归式:

\[ \psi(x)=\sum_k\sqrt{2}\varphi(2x-k) \]

其中$h_\psi(k)$系数称为(小波函数系数)

小波级数展开:

\[ f(x)=\sum_kc_{j_0}(k)\varphi_{j_0,k}(x)+\sum_{j=j_0}^{\infty}\sum_kd_j(k)\psi_{j,k}(x) \]

式中, $c_{j_0}$和$d_j,j\ge j_0$分别称为近似系数和细节系数, 若尺度和小波函数规范正交, 则有:

\[ \begin{gather} c_{j_0}=\left\langle f(x),\varphi_{j_0,k}(x)\right\rangle \\ d_j=\left\langle f(x),\psi_{j,k}(x)\right\rangle \end{gather} \]

利用了正交性

对于$y=x^2$的哈尔小波展开

\[ y=\left\{ \begin{matrix} x^2,&0\le x\le 1\\ 0,&other \end{matrix} \right. \]

采用哈尔小波计算

\[ \begin{align} c_0(0)&=\int_0^1x^2\varphi_{0,0}(x)\text{d}x=\int_0^1x^2\text{d}x=\left.\frac{x^2}{3}\right|_0^1=\frac{1}{3}\\ d_0(0)&=\int_0^1x^2\psi_{0,0}(x)\text{d}x=\int_0^{0.5}x^2\text{d}x-\int_{0.5}^1x^2\text{d}x=-\frac{1}{4}\\ d_1(0)&=\int_0^1x^2\psi_{1,0}(x)\text{d}x=\int_0^{0.25}x^2\sqrt{2}\text{d}x-\int_{0.25}^{0.5}x^2\sqrt{2}\text{d}x=-\frac{1}{4}=-\frac{\sqrt{2}}{32}\\ d_1(1)&=\int_0^1x^2\psi_{1,1}(x)\text{d}x=\int_{0.5}^{0.75}x^2\sqrt{2}\text{d}x-\int_{0.75}^{1}x^2\sqrt{2}\text{d}x=-\frac{1}{4}=-\frac{3\sqrt{2}}{32} \end{align} \]

带入展开函数可得到:

\[ y= \sideset{}{}{\underbrace{ \sideset{}{}{\underbrace{ \sideset{}{}{\underbrace{\frac{1}{3}\varphi_{0,0}(x)}}_{V_0} + \sideset{}{}{\underbrace{\left[-\frac{1}{4}\psi_{0,0}(x)\right]}}_{W_0} }}_{V_1=V_0\oplus W_0} + \sideset{}{}{\underbrace{\left[-\frac{\sqrt{2}}{32}\psi_{1,0}(x)-\frac{3\sqrt{2}}{32}\psi_{1,1}(x)\right]}}_{W_1} }}_{V_2=V_1\oplus W_1=V_0\oplus W_0\oplus W_1} + \cdots \]

一维离散小波变换

\[ f(x)=\frac{1}{\sqrt{N}}\left[T_{\varphi}(0,0)\varphi(x)+\sum_{j=0}^{J-1}\sum_{k=0}^{2^j-1}T_{\psi}(j,k)\psi_{j,k}(x)\right] \]

其中

\[ T_\varphi(0,0)=\left\langle f(x),\varphi_{0,0}(x)\right\rangle=\left\langle f(x),\varphi(x)\right\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}f(x)\varphi^*(x) \]

\[ T_\psi(j,k)=\left\langle f(x),\psi_{j,k}(x)\right\rangle=\frac{1}{\sqrt{N}}\sum_{x=0}^{N-1}f(x)\psi^*_{j,k}(x) \]

$*$代表共轭, 第一个系数代表近似系数, 第二个代表细节系数, 如果尺度函数和小波函数的值是实数, 那么可以消除共轭, 如果基是双正交的, 则上两式中的$\varphi$和$\psi$必须由他们的对偶$\tilde{\varphi}$和$\tilde{\psi}$代替

$V_0$和$W_0$的基可以是双正交, 也可以是$V_0$的基为$W_0$的低尺度变换基

快速小波变换:

通过$\varphi$和$\psi$的迭代可以

展开系数:

\[ \begin{gather} c_j(k)=\sum_nh_{\varphi}(n-2k)c_{j+1}(n)\\ d_j(k)=\sum_nh_{\psi}(n-2k)c_{j+1}(n)\\ \end{gather} \]

得到的变换结果:

\[ \begin{gather} T_{\varphi}(j,k)=\sum_nh_{\varphi}(n-2k)T_{\varphi}(j+1,n)\\ T_{\psi}(j,k)=\sum_nh_{\psi}(n-2k)T_{\psi}(j+1,n) \end{gather} \]

对于离散的小波变换:

\[ \begin{gather} T_{\varphi}(j,k)=T_{\varphi}(j+1,n)\bigstar h_{\varphi}(-n)\\ T_{\psi}(j,k)=T_{\psi}(j+1,n)\bigstar h_{\psi}(-n) \end{gather} \]

分析滤波器组:

\[ T_{\varphi}(j+1,k)\rightarrow\left\{ \begin{matrix} \bigstar h_{\psi}(-n)&\rightarrow&2\downarrow&\rightarrow&T_{\psi}(j,k)\\ \bigstar h_{\varphi}(-n)&\rightarrow&2\downarrow&\rightarrow&T_{\varphi}(j,k) \end{matrix} \right. \]

对于多尺度的, 接着对$T_{\varphi}(j,k)$进行分析

二维小波变换:

二维需要1个二维尺度函数$\varphi(x,y)$和3个二维小波函数$\psi^H(x,y),\psi^V(x,y),\psi^D(x,y)$分别代表垂直水平对角, 每个二维小波都是两个一维函数的积排除$\varphi(x)\psi(x)$, 剩下可分离的尺度函数:

\[ \varphi(x,y)=\varphi(x)\varphi(y) \]

和可分离的”方向敏感小波”:

\[ \begin{gather} \psi^H(x,y)=\psi(x)\varphi(y)\\ \psi^V(x,y)=\varphi(x)\psi(y)\\ \psi^D(x,y)=\psi(x)\psi(y) \end{gather} \]

\[ T_{\varphi}(j+1,k)\rightarrow\left\{ \begin{matrix} \bigstar h_{\psi}(-n)\rightarrow2\downarrow\rightarrow \left\{ \begin{matrix} \bigstar h_{\psi}(-m)\rightarrow2\downarrow\rightarrow T_{\psi}^D(j,k)\\ \bigstar h_{\varphi}(-m)\rightarrow2\downarrow\rightarrow T_{\psi}^V(j,k) \end{matrix} \right. \\ \bigstar h_{\varphi}(-n)\rightarrow2\downarrow\rightarrow \left\{ \begin{matrix} \bigstar h_{\psi}(-m)\rightarrow2\downarrow\rightarrow T_{\psi}^H(j,k)\\ \bigstar h_{\varphi}(-m)\rightarrow2\downarrow\rightarrow T_{\varphi}(j,k) \end{matrix} \right. \end{matrix} \right. \]

排布:

\[ \begin{matrix} T_{\varphi}&T_{\psi}^H\\ T_{\psi}^V&T_{\psi}^D\\ \end{matrix} \]

8 图像压缩和水印

9 形态学图像处理

反射: 结构元旋转180°

腐蚀:

\[ A\ominus B=\{z|(B)_z\subseteq A\} \]

$A$为前景像素的集合, $B$为结构元, z是前景像素值(结构元中的点)

等效于

\[ I\circleddash B=\{z|(B)_z\subseteq A,A\subseteq I\}\cup\{A^c|A^c\subseteq I\} \]

\[ A\ominus B=\left\{z|(B)_z\cap A^c=\varnothing\right\} \]

$A^c$为补集

腐蚀可以增强图像细的目标, 删除前景图像中小于结构元的部分

膨胀:

\[ A\oplus B=\{z|(\hat{B})_z\cap A\neq \varnothing\} \]

$\hat{B}$为$B$的反射, 所有和$A$相交的位移点集合

等效于

\[ A\oplus B=\{z|[(\hat{B})_z\cap A]\subseteq A\} \]

膨胀运算类似于二维图像卷积, $B$为卷积核

膨胀可以增长粗化图像中的目标, 用于修复断裂字符等

对偶性:

\[ (A\ominus B)^c=A^c\oplus B^c \]

\[ (A\oplus B)^c=A^c\ominus B^c \]

开运算:

\[ A\circ B=(A\ominus B)\oplus B=\cup\{(B)_z|(B)_z\subseteq A\} \]

闭运算:

\[ A\bullet B=(A\oplus B)\ominus B=[\cup(B)_z|(B)_z\cap A=\varnothing]^c \]

开运算闭运算对偶:

\[ (A\circ B)^c=(A^c\bullet B^c) \]

\[ (A\bullet B)^c=(A^c\circ B^c) \]

开运算性质:

$A\circ B\subseteq A$
若$C\subseteq D$, $C\circ B\subseteq D\circ B$
$(A\circ B)\circ B=A\circ B$

闭运算性质:

$A\bullet B\subseteq A$
若$C\subseteq D$, $C\bullet B\subseteq D\bullet B$
$(A\bullet B)\bullet B=A\bullet B$

击中-击不中变换(HMT):

两个结构元, 前景中检测形状$B_1$, 背景中检测形状$B_2$:

\[ I\circledast B_{1,2}=\{z|(B_1)_z\subseteq A, (B_2)_z\subseteq A^c\}=(A\ominus B_1)\cap(A^c\ominus B_2) \]

其中$B_1\cap B_2=\varnothing$

目的是为了检测在$A$中和$B_1$一模一样的元, $B_2$为$B_1$膨胀1后减去$B_1$的元, 最终的结果是匹配到的结构元的选定的代表结构元的点, 最终结果是位置点

形态学算法

边界提取:

\[ \beta(A)=A-(A\ominus B) \]

孔洞填充:

\[ X_k=(X_{k-1}\oplus B)\cap I^c,\qquad k=1,2,3,\cdots \]

其中$X_0$为孔洞中的一个点, 需要提前给出

连通量提取:

\[ X_k=(X_{k-1}\oplus B)\cap I,\qquad k=1,2,3,\cdots \]

其中$X_0$为前景上面的一个点, 根据这个点在前景上扩展直到不在增加, 对于4连通域要用4连通域的结构元, 对于8连通域要用8连通域的结构元

凸壳:

点集$S$是凸的定义是: 连接$S$内任意两点的直线段完全在$S$内, 凸壳$H$是包含$S$的最小凸集

\[ X_k^i=(X_{k-1}^i\circledast B^i)\cup X_{k-1}^i,\qquad i=\{1,2,3,4\},k=1,2,3,\cdots \]

结构元如图:

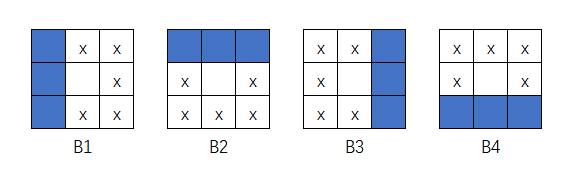
图中的x代表不管有没有匹配到x都可以, 但是没有x的代表必须没有

原理:

比如$B_1$, 在原图上检测到三个像素一列, 就会在三个像素中间的右侧填充前景色迭代下去

四个方向最终运算的结果会是一个四边形, 但是根据原始图像的四个方向的最边缘像素可以截取掉多余的部分

细化:

\[ A\otimes B=A-(A\circledast B)=A\cap (A\circledast B)^c \]

而$B$由一系列的结构元组成

\[ A\otimes \{B\}=((\cdots((A\otimes B^1)\otimes B^2))\otimes B^n) \]

$A$从被$B^1$一直到$B^n$细化, 然后再重复, 直到所有的结构元都不能细化为止

结构元如图:

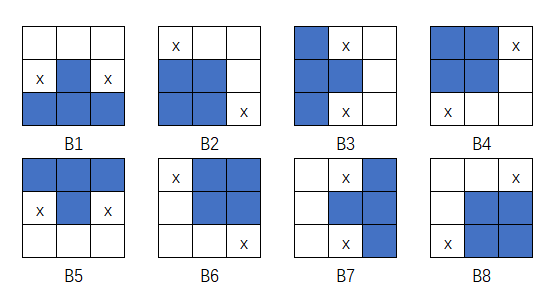
对于上下左右来说, 细化是凸壳的类似逆运算, 会舍弃匹配到的一列(横,竖,斜), 对于数字图像来说

骨架:

集合$A$的骨架$S(A)$

若$z$是$S(A)$的一点, $(D)_z$是以$z$为圆心的最大圆盘, 则不存在包含$(D)_z$且位于$A$内的更大圆盘(不必以$z$为中心). 满足这些条件的圆盘$(D)_z$称为最大圆盘
若$(D)_z$是一个最大圆盘, 则它在两个或多个不同位置与$A$的边界接触

$A$的骨架可以用开运算表示:

\[ S(A)=\bigcup_{k=0}^KS_k(A) \]

\[ S_k(A)=(A\ominus kB)-(A\ominus kB)\circ B \]

每次被开运算去掉的部分的集合

裁剪:

消除噪声引起骨架的寄生部分

形态学重建:

根据标记点, 在原图前景处不断扩散直到不能扩散, 用处比如在带字的图像上取单个字符

测地膨胀

\[ D_G^{(1)}(F)=(F\oplus B)\cap G \]

$F$为标记图像, $G$为模板图像, 根据模板图像的以标记点为中心膨胀

对于大小为$n$的测地膨胀

\[ D_G^{(n)}(F)=D_G^{(1)}\left[D_G^{(n-1)}(F)\right] \]

测地腐蚀

\[ E_G^{(1)}(F)=(F\ominus B)\cup G \]

$F$为标记图像, $G$为模板图像, 根据模板图像将标记图像不断腐蚀

\[ E_G^{(n)}(F)=E_G^{(1)}\left[E_G^{(n-1)}(F)\right] \]

标记$F$对模板图像$G$的膨胀形态学重建为

\[ R_G^D(F)=D_G^k(F) \]

腐蚀形态学重建

\[ R_G^E(F)=E_G^k(F) \]

灰度形态学

灰度腐蚀

\[ [f\ominus b](x,y)=\min_{(s,t)\in b}\{f(x+s,y+t)\} \]

灰度膨胀

\[ [f\oplus b](x,y)=\max_{(s,t)\in b}\{f(x-s,y-t)\} \]

其中$(x-s,y-t)$相当于结构元旋转了180°

灰度开运算闭运算

和二值图像相同

灰度级形态学算法

形态学平滑

使用先做开运算后做闭运算

形态学梯度

\[ g=(f\oplus b)-(f\ominus b) \]

顶帽变换和底帽变换

顶帽

\[ T_{hat}(f)=f-(f\circ b) \]

底帽

\[ B_{hat}(f)=(f\bullet b)-f \]

例子, 用顶帽变换校正阴影用于阈值分割, 基于Otsu最优阈值会因为阴影出现错误

粒度测量

纹理分割

灰度形态学重建

2 数字图像基础#

3 灰度变换与空间滤波#

4 频率域滤波#

5 图像复原与重建#

6 彩色图像处理#

7 小波变换和其他图像变换#

8 图像压缩和水印#

9 形态学图像处理#