## 初识SLAM
flowchart LR
sensor(传感器数据)
frontEnd(前端视觉里程计)
backEnd(后端非线性优化)
mapping(建图)
loopClosing(回环检测)
sensor-->frontEnd-->backEnd-->mapping
sensor-->loopClosing-->backEnd步骤:
-
传感器数据读取
-
视觉里程计(Visual Odometry, VO)。估计相邻图像间相机的运动,以及局部地图的样子。主要用到图像特征提取和匹配
-
后端优化(Optimization)。接受不同时刻视觉里程计测量的相机位姿,以及回环检测的信息,对它们进行优化,得到全局一致的轨迹和地图。需要消除噪声问题,用到滤波和非线性优化算法
-
回环检测(Loop Closing)。判断机器人是否打到过先前位置,检测到回环提交给后端处理。SLAM时会出现累计误差需要回环检测消除
-
建图(Mapping)。根据估计的轨迹,建立任务对应的地图
VIO:视觉惯性里程计,视觉里程计+IMU
数学问题表述
用$x$表示机器人位置,离散时刻位置记为$x_1,\ldots,x_k$,构成轨迹,每个时刻传感器会测量到一部分路标点一共有N个,用$y_1,\ldots,y_N$表示
- 运动:考察从$k-1$时刻到$k$时刻,机器人的位置$x$的变化
- 观测:描述机器人在$k$时刻处于$x_k$位置处探测到了路标$y_i$
运动方程:
$$ x_k=f(x_{k-1},u_k,w_k) $$$u_k$为运动传感器读数或者输出,$w_k$为噪声
观测方程:
$$ z_{k,j}=h(y_j,x_k,v_{k,j}) $$机器人在$x_k$位置看到路标$y_j$产生了观测数据$z_{k,j}$,$v_{k,j}$为噪声
三维空间刚体运动
矩阵变换
欧式变换
$$ \left [ e_1,e_2,e_3 \right ]\begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = \left [ e_1' ,e_2',e_3' \right ]\begin{bmatrix} a_1' \\ a_2' \\ a_3' \end{bmatrix} $$不同坐标系下向量$a$的坐标,两边乘$\begin{bmatrix} {e_1}^{T} \\ {e_2}^{T} \\ {e_3}^{T} \end{bmatrix}$可得到
$$ \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} = \begin{bmatrix} e_1^T e_1^′ & e_1^T e_2^′ & e_1^T e_3^′ \\ e_2^T e_1^′ & e_2^T e_2^′ & e_2^T e_3^′ \\ e_3^T e_1^′ & e_3^T e_2^′ & e_3^T e_3^′ \end{bmatrix} \begin{bmatrix} a_1 \\ a_2 \\ a_3 \end{bmatrix} \triangleq Ra' $$矩阵$R$为 旋转矩$\Leftrightarrow$阵行列式为1的正交矩阵,定义
$$ \mathrm{SO}(n)=\left \{\boldsymbol{R}\in \mathbb{R}^{n\times n}|\boldsymbol{RR}^T=I,\det(\boldsymbol{R})=1\right \} $$$$ \boldsymbol R^{-1}a=\boldsymbol R^Ta $$特殊正交群(Special Orthogonal Group)
加上平移向量
$$ \boldsymbol{a'= Ra+ t} $$变换
$$ \boldsymbol{b= R_1a+ t_1,\space c= R_2b+ t_2} $$a到c变换为
$$ \boldsymbol{c=R_2( R_1a+ t_1)+ t_2} $$变换后会很不方便,使用齐次坐标和变换矩阵
$$ \begin{bmatrix} \boldsymbol a' \\ 1 \end{bmatrix} = \begin{bmatrix} \boldsymbol {R} & \boldsymbol{t} \\ 0^T & 1 \end{bmatrix} \begin{bmatrix} \boldsymbol a \\ 1 \end{bmatrix} \triangleq \boldsymbol{T} \begin{bmatrix} \boldsymbol a \\ 1 \end{bmatrix} $$$\boldsymbol T$为变换矩阵
$$ \mathrm{SE}(3)= \left \{T= \begin{bmatrix} R & t\\ 0^T & 1 \end{bmatrix} \in \mathbb{R}^{4\times 4} | R \in \mathrm{SO}(3), t\in \mathbb{R}^3 \right \} $$$$ T^{-1}=\begin{bmatrix} R^T & -R^Tt\\ 0^T & 1 \end{bmatrix} $$特殊欧氏群(Special Euclidean Group)
Eigen库
旋转向量和欧拉角
矩阵冗余
旋转轴用单位向量$n$表示,角度用$\theta$表示
和矩阵变换的关系:罗德里格斯公式(Rodrigues’s Formula)
$$ \boldsymbol R=\cos \theta \boldsymbol I + (1-\cos \theta)\boldsymbol n\boldsymbol n^T+\sin \theta \boldsymbol n^\wedge $$$n^\wedge$是向量到反对称矩阵的转换符
$$ \boldsymbol a\times \boldsymbol b= \begin{Vmatrix} e_1 & e_2 & e_3 \\ a_1 & a_2 & a_3 \\ b_1 & b_2 & b_3 \end{Vmatrix} = \begin{bmatrix} a_2b_3-a_3b_2 \\ a_3b_1-a_1b_3 \\ a_1b_2-a_2b_1 \end{bmatrix} = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} \boldsymbol b \triangleq \boldsymbol a^\wedge \boldsymbol b $$$$ \boldsymbol a^\wedge = \begin{bmatrix} 0 & -a_3 & a_2 \\ a_3 & 0 & -a_1 \\ -a_2 & a_1 & 0 \end{bmatrix} $$罗德里格斯公式两边取迹(矩阵对角线元素之和)
$$ \begin{align*} \mathrm{tr}(\boldsymbol R)= & \cos\theta \space\mathrm{tr}(\boldsymbol I) + (1-\cos\theta)\space \mathrm{tr}(\boldsymbol n \boldsymbol n^T)+\sin\theta \space \mathrm{tr}(\boldsymbol n^\wedge) \\ \space = & 3\cos\theta + (1-\cos\theta)\\ = & 1+2\cos\theta \end{align*} $$转轴$n$旋转$n$方向的向量结果不变
$$ \boldsymbol R\boldsymbol n= \boldsymbol n $$转轴$\boldsymbol n$是矩阵$\boldsymbol R$特征值1对应的特征向量,求解方程归一化得到$\boldsymbol n$
欧拉角
- yaw:偏航角,物体绕z轴旋转
- pitch:俯仰角,绕y轴旋转的
- roll:滚转角,绕x轴旋转
欧拉角的转动是按轴顺序来的
RPY角(xyz顺序)和Euler角(zyx)
万向锁
四元数
旋转矩阵冗余,欧拉角和旋转向量紧凑但是有奇异性
四元数有一个实部三个虚部
$$ q=q_0+q_1i+q_2j+q_3k $$满足
$$ \begin{cases} i^2=j^2=k^2=-1 \\ ij=k, ji=-k \\ jk=i, kj=-i \\ ki=j, ik=-j \end{cases} $$用标量和向量表示四元数
$$ q=[s,v]^T,\quad s=q_0\in\mathbb{R},\quad v=[q_1,q_2,q_3]^T\in\mathbb{R^3} $$$s$为四元数实部,$v$为四元数虚部,如果一个四元数的虚部为0,称之为实四元数。反 之,若它的实部为0,则称之为虚四元数
乘以$i$意味着旋转180°,$ij=k$
坐标轴记忆,从xyz都为正的象限看向原点,xyz轴呈逆时针顺序
运算
$$ q_a=s_a +x_ai + y_aj + z_ak, \quad q_b=s_b+x_bi+y_bj+z_bk $$- 加法减法
- 乘法
每项分别相乘然后相加,总共16项,虚部乘法转换要按照运算关系
$$ \begin{align*} q_aq_b=&s_as_b-x_ax_b-y_ay_b-z_az_b\\ +&(s_ax_b+x_as_b+y_az_b-z_ay_b)i\\ +&(s_ay_b-x_az_b+y_as_b+z_ax_b)j\\ +&(s_az_b+x_ay_b-y_ax_b+z_as_b)k \end{align*} $$$$ q_aq_b=[s_as_b-v_a^Tv_b,s_av_b+s_bv_a+v_a\times v_b]^T $$乘法不具备交换律
- 模长
四元数乘积的模长等于模长的乘积
$$ \|q_aq_b\|=\|q_a\|\|q_b\| $$- 共轭
把虚部向量取反
$$ q_a^*=[s_a,-v_a]^T $$$$ q^*q=qq^*=[s_a+v^Tv,0]^T $$得到实四元数
- 逆
四元数为单位四元数,其逆和共轭是一个量
$$ q_I^{-1}=q_I^{*} $$乘积的逆具有类似矩阵的性质
$$ (q_aq_b)^{-1}=q_b^{-1}q_a^{-1} $$- 数乘
表示旋转
点用四元数描述
$$ p=[0,x,y,z]^T=[0,v]^T $$旋转后的点为
$$ p'=qpq^{-1} $$然后把$p'$虚部取出来
其他旋转转换到四元数
四元素乘法写成矩阵乘法
$$ q^+=\begin{bmatrix} s & -v^T\\ v & sI+v^\wedge \end{bmatrix}, \quad q^{\oplus}=\begin{bmatrix} s & -v^T\\ v & sI-v^\wedge \end{bmatrix} $$$$ q_1^+q_2=\begin{bmatrix} s & -v^T\\ v & sI+v^\wedge \end{bmatrix} \begin{bmatrix} s_2\\ v_2 \end{bmatrix} = \begin{bmatrix} -v_1^Tv_2+s_1s_2\\ s_1v_2+s_2v_1+v_1^\wedge v_2 \end{bmatrix} = q_1q_2 $$可以证明
$$ q_1q_2=q_1^+q_2=q_2^\oplus q_1 $$$$ \begin{align*} p'=&qpq^{-1}=q^+p^+q^{-1}\\ =&q^+{q^{-1}}^\oplus p \end{align*} $$带入矩阵计算
$$ q^+{(q^{-1})}^\oplus=\begin{bmatrix} s & -v^T \\ v & sI+v^\wedge \end{bmatrix} \begin{bmatrix} s & v^T \\ -v & sI+v^\wedge \end{bmatrix}= \begin{bmatrix} 1 & 0 \\ 0^T & vv^T+s^2I+2sv^\wedge+(v^\wedge)^2 \end{bmatrix} $$$$ R=vv^T+s^2I+2sv^\wedge+(v^\wedge)^2 $$两边求迹
$$ \begin{align*} \mathrm{tr}(R)&=\mathrm{tr}\left (vv^T+s^2I+2sv^\wedge+(v^\wedge)^2\right)\\ &=v_1^2+v_2^2+v_3s^2+3s^2-2(v_1^2+v_2^2+v_3^2)\\ &=(1-s^2)+3s^2-2(1-s^2)\\ &=4s^2-1 \end{align*} $$$$ \begin{align*} \theta&=\arccos\left(\frac{\mathrm{tr}(R-1)}{2}\right)\\ &=\arccos(2s^2-1) \end{align*} $$$$ \begin{cases} \theta=2\arccos s\\ [n_1,n_2,n_3]^T=[q_1,q_2,q_3]^T/\sin\frac{\theta}{2} \end{cases} $$3D变换
- 相似变换
$R$部分缩放
$$ T_s=\begin{bmatrix} sR &t\\ 0^T & 1 \end{bmatrix} $$- 仿射
$R$矩阵不再正交,只要求可逆
$$ T_s=\begin{bmatrix} A &t\\ 0^T & 1 \end{bmatrix} $$- 射影
$A$可逆,$a^T$缩放,$t$平移
Pangolin基于OpenGL的绘图库
李群与李代数
基础
群
$$ \mathrm{SO}(3)=\left \{\mathbf{R}\in \mathbb{R}^{3\times 3}|RR^T=I,\det(R)=1\right \} $$$$ \mathrm{SE}(3)= \left \{T= \begin{bmatrix} R & t\\ 0^T & 1 \end{bmatrix} \in \mathbb{R}^{4\times 4} | R \in \mathrm{SO}(3), t\in \mathbb{R}^3 \right \} $$对加法不封闭
$$ R_1+R_2\notin \mathrm{SO}(3),\quad T_1+T_2\notin\mathrm{SE}(3) $$乘法是封闭的
$$ R_1R_2\in \mathrm{SO}(3),\quad T_1T_2\in\mathrm{SE}(3) $$群(Group)是一种集合加上运算的代数结构,集合记为$A$,群记作$G=(A,\cdot)$,满足:
- 封闭性:$\forall a_1,a_2\in A,\quad a_1\cdot a_2\in A$
- 结合律:$\forall a_1,a_2,a_3\in A,\quad (a_1\cdot a_2)\cdot a_3=a_1\cdot (a_2\cdot a_3)$
- 幺元:$\exists a_0\in A,\quad \mathrm{s.t.}\quad \forall a\in A, \quad a_0\cdot a=a\cdot a_0=a$
- 逆:$\forall a\in A, \quad \exists a^{-1}\in A, \quad \mathrm{s.t.} \quad a\cdot a^{-1}=a_0$
李群是指具有连续性质的群,整数$\mathbb{Z}$没有
李代数
对于旋转矩阵
$$ RR^T=I $$$R$随时间变化,则
$$ R(t)R(t)^T=I $$等式两边求导,得到:
$$ \dot{R}(t)R(t)^T+R(t)\dot{R}(t)^T=0 $$$$ \dot{R}(t)R(t)^T=-(R(t)\dot{R}(t)^T)^T $$$\dot{R(t)}R(t)^T$是一个反对称矩阵,所以存在一个向量和反对称矩阵对应
$$ a^\wedge=A=\begin{bmatrix} 0 & -a_3 & a_2\\ a_3 & 0 & -a_1\\ -a_2 & a_1 & 0 \end{bmatrix},\quad A^{\vee}=a $$设这个三维向量为$\phi(t)\in \mathbb{R}^3$,则
$$ \dot{R}(t)R(t)^T=\phi(t)^\wedge $$两边右乘$R(t)$得到
$$ \dot{R}(t)=\phi(t)^\wedge R(t)=\begin{bmatrix} 0 & -\phi_3 & \phi_2\\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix} R(t) $$$R(t)$在$t=0$附近的一阶泰勒展开
$$ \textit{\textbf{text}} \begin{align*} R(t)&\approx R(t_0)+\dot{R}(t_0)(t-t_0)\\ &=I+\phi(t_0)^\wedge(t) \end{align*} $$$\phi$反映了$R$的导数性质,故称它在$\mathrm{SO}(3)$原点附近的正切空间(Tangent Space)上,在$t_0$附近,有
$$ \dot{R}(t)=\phi(t_0)^\wedge R(t)=\phi_0^\wedge R(t) $$解微分方程,类似于$f'(x)=kf(x)$,得到
$$ R(t)=e^{\phi_0^\wedge t} $$总结:
- 给定某时刻的$R$就能求得一个$\phi$,$\phi$是对应到$\mathrm{SO}(3)$上的李代数$\mathfrak{so}(3)$
- 引出李群与李代数间的指数/对数映射
李代数定义
李代数由一个集合$\mathbb{V}$,一个数域$\mathbb{F}$和一个二元运算$[,]$组成,如果它们满足以下几条性质,则称$(\mathbb{V},\mathbb{F},[,])$为一个李代数,记作$\mathfrak{g}$。
- 封闭性 $\forall X,Y\in\mathbb{V},[X,Y]\in\mathbb{V}$
- 双线性 $\forall X,Y,Z\in\mathbb{V},a,b\in\mathbb{F}$,有
- 自反性 $\forall X\in\mathbb{V},[X,X]=0$
- 雅可比等价 $\forall X,Y,Z\in\mathbb{V},[X,[Y,Z]]+[Z,[X,Y]]+[Y,[Z,X]]=0$
二元运算被称为李括号
李代数$\mathfrak{so}(3)$
$$ \mathit{\Phi}=\phi^\wedge=\begin{bmatrix} 0 & -\phi_3 & \phi_2\\ \phi_3 & 0 & -\phi_1\\ -\phi_2 & \phi_1 & 0 \end{bmatrix}\in\mathbb{R}^{3\times 3} $$李括号的定义
$$ [\phi_1,\phi_2]=(\mathit{\Phi}_1\mathit{\Phi}_2-\mathit{\Phi}_2\mathit{\Phi}_1)^{\wedge} $$六维向量,前三维平移(和矩阵不一样),记作$\rho$,后三维为旋转,记作$\phi$,对于$\xi^\wedge$,扩展了反对称的用法
$$ \xi^\wedge=\ \begin{bmatrix} \phi^\wedge & \rho\\ 0^T & 0 \end{bmatrix} \in \mathbb{R}^{4\times 4} $$$$ [\xi_1,\xi_2]=(\xi_1^\wedge\xi_2^\wedge-\xi_2^\wedge\xi_1^\wedge) $$指数与对数映射
$\mathfrak{so}(3)$上的指数映射
任意矩阵的指数映射可以泰勒展开,在收敛的情况下仍然是一个矩阵
$$ \exp(A)=\sum^\infty_{n=0}\frac{1}{n!}A^n $$$$ \exp(\phi^\wedge)=\sum^\infty_{n=0}\frac{1}{n!}(\phi^\wedge)^n $$用向量定义$\phi$,有$\phi=\theta a,\space\|a\|=1$
$$ a^\wedge a^\wedge=\begin{bmatrix} -a_2^2-a_3^2 & a_1a_2 & a_1a_3\\ a_1a_2 & -a_1^2-a_3^2 & a_2a_3\\ a_1a_3 & a_2a_3 & -a_1^2-a_2^2 \end{bmatrix}=aa^T-I $$$$ a^\wedge a^\wedge a^\wedge =a^\wedge(aa^T-I)=-a^\wedge $$由此可以得到$a^\wedge$的n次的结果
$$ \begin{align*} \exp(\phi^\wedge)&=\sum^\infty_{n=0}\frac{1}{n!}(\theta a^\wedge)^n\\ &=I+\theta a^\wedge-a^\wedge a^\wedge + \theta a^\wedge + \frac{1}{2!}\theta^2 a^\wedge a^\wedge +\frac{1}{3!} (a^\wedge)^3 +\frac{1}{4!} (a^\wedge)^4 + \ldots\\ &=aa^T- a^\wedge a^\wedge +\theta a^\wedge + \frac{1}{2!}\theta^2 a^\wedge a^\wedge -\frac{1}{3!} a^\wedge -\frac{1}{4!} (a^\wedge)^2\\ &=aa^T+\sideset{}{}{\underbrace{\left( \theta - \frac{1}{3!}\theta^3+\frac{1}{5!}\theta^5+\ldots \right )}}_{\sin \theta}a^\wedge-\sideset{}{}{\underbrace{\left( 1 - \frac{1}{2!}\theta^2+\frac{1}{4!}\theta^4+\ldots \right )}}_{\cos \theta}a^\wedge a^\wedge\\ &=a^\wedge a^\wedge + I+\sin\theta a^\wedge - \cos\theta a^\wedge a^\wedge\\ &=(1-\cos\theta)a^\wedge a^\wedge+I+\sin\theta a^\wedge\\ &=\cos\theta+(1-\cos\theta)aa^T+\sin\theta a^\wedge \end{align*} $$最后得到:
$$ \exp(\theta a^\wedge)=\cos\theta+(1-\cos\theta)aa^T+\sin\theta a^\wedge $$和罗德公式一样
$\mbox{SE}(3)$上的指数映射
$$ \begin{align*} \exp{\xi^\wedge}&=\begin{bmatrix} \sum_{n=0}^{\infty}\frac{1}{n!}(\phi^\wedge)^n & \sum_{n=0}^{\infty}\frac{1}{(n+1)!}(\phi^\wedge)^n\rho\\ 0^T & 1 \end{bmatrix} \\ &\triangleq\begin{bmatrix} R & J\rho\\ 0^T & 1 \end{bmatrix} = T \end{align*} $$同样的展开方式求得
$$ J=\frac{\sin\theta}{\theta}I+\left(1-\frac{\sin\theta}{\theta}\right)aa^T+\frac{1-\cos\theta}{\theta}a^\wedge $$最后总结李群和李代数的关系
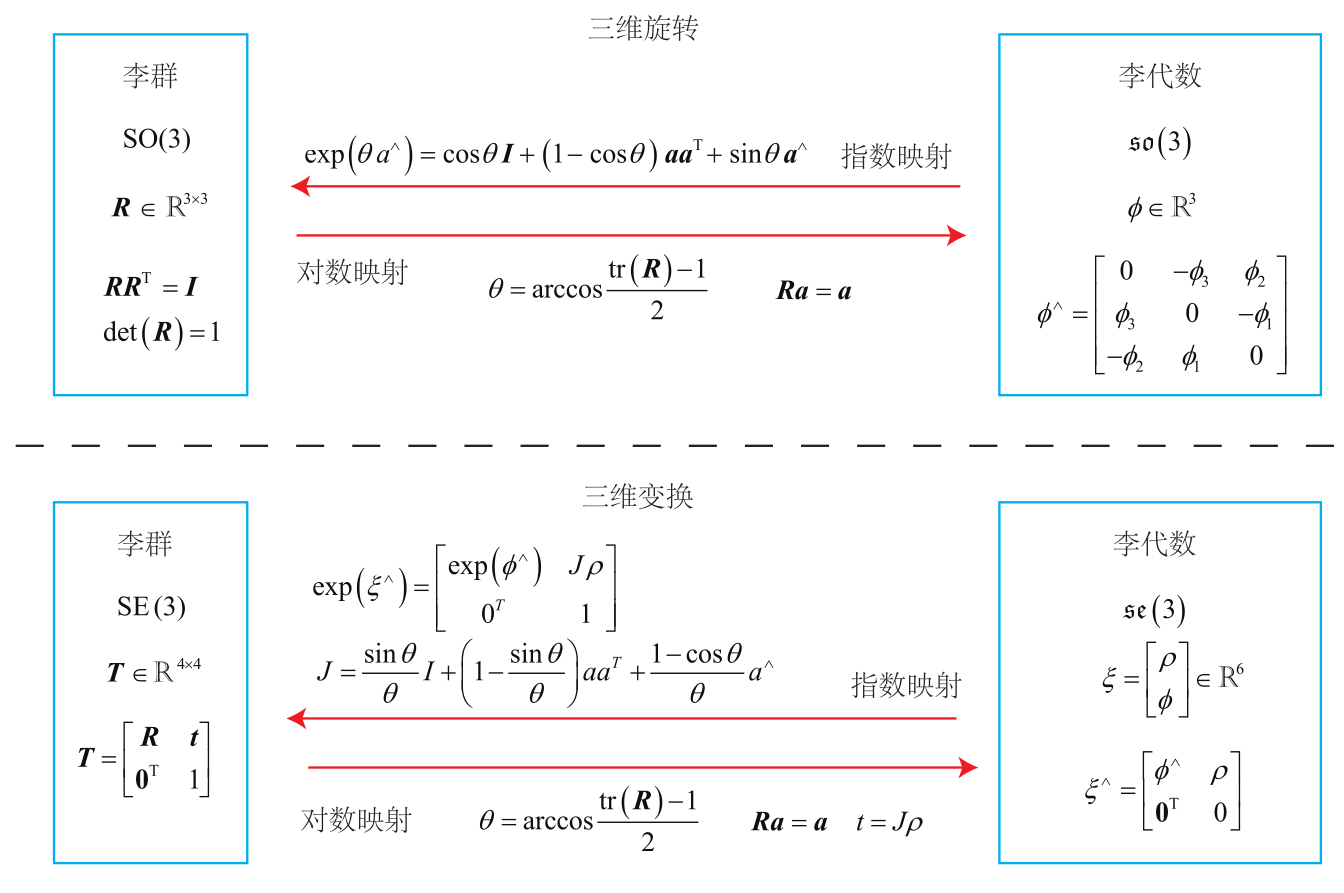
李代数求导和扰动模型
Sophus
相机与图像
相机模型
透镜产生畸变,根据模型计算内参
针孔相机模型
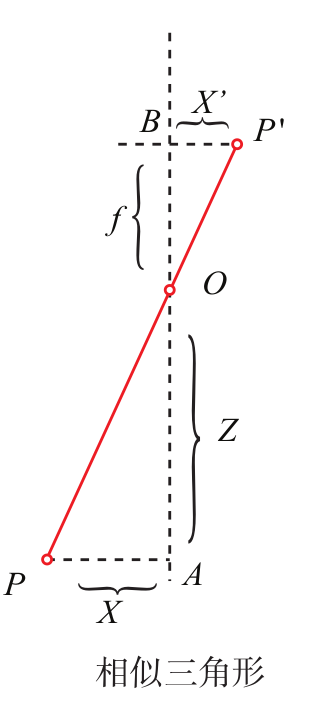
$X$为物体大小,$X'$为图像大小
$$ \frac{Z}{f}=-\frac{X}{X'}=-\frac{Y}{Y'} $$所以得到
$$ \begin{cases} X'=f\frac{X}{Z}\\ Y'=f\frac{Y}{Z} \end{cases} $$像素坐标:
$$ [u,v]^T $$原点定义为图像的左上角,和成像平面多了缩放和原点的平移
所以得到
$$ \begin{cases} u=\alpha X'+c_x\\ v=\beta Y' + c_y \end{cases} $$$$ \begin{cases} u=f_x \frac{X}{Z}+c_x\\ v=f_y \frac{Y}{Z} + c_y \end{cases} $$改成齐次坐标变换
$$ \begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\frac{1}{Z}\begin{pmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\triangleq\frac{1}{Z}KP $$$$ Z\begin{pmatrix} u\\ v\\ 1 \end{pmatrix}=\begin{pmatrix} f_x & 0 & c_x\\ 0 & f_y & c_y\\ 0 & 0 & 1 \end{pmatrix}\begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\triangleq KP $$$K$为内参矩阵,一般出厂后是固定的,标定方法有单目棋盘格张正友标定法
相机的外参$R,t$为相机的旋转平移量,$P=RP_w+t$
投影过程可以看成把世界坐标点转换到相机坐标系,再去掉相机z轴方向的数值
畸变
透镜形状引起的畸变称为径向畸变,分为桶形畸变和枕形畸变
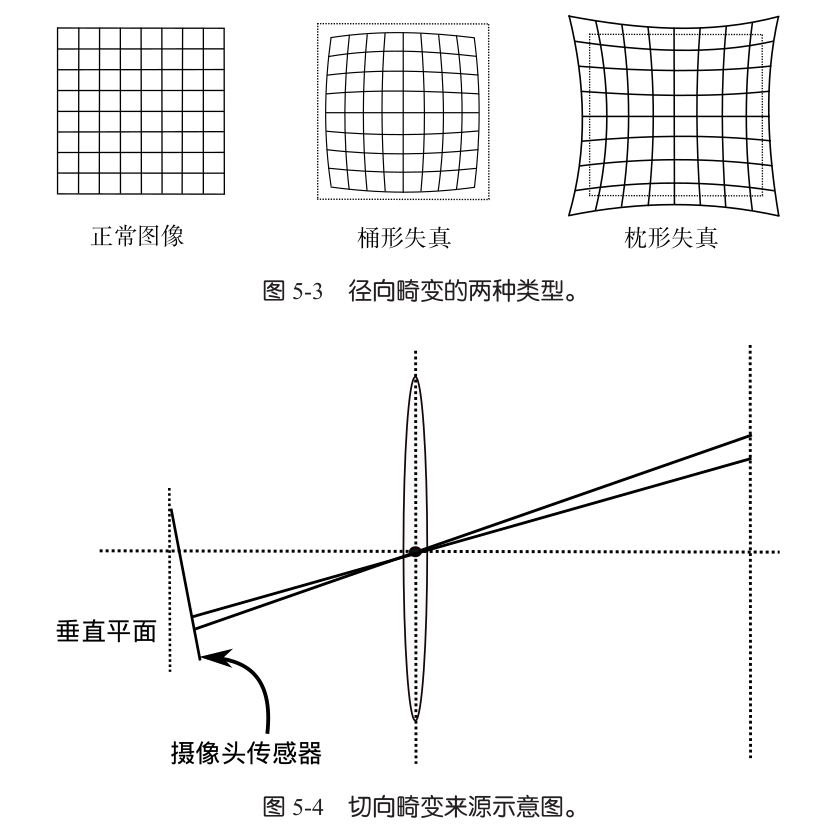
切向畸变来源为透镜和成像平面不平行
径向畸变多项式关系:
$$ \begin{align} x_\text{distorted}=x(1+k_1r^2+k_2r^4+k_3r^6)\\ y_\text{distorted}=y(1+k_1r^2+k_2r^4+k_3r^6) \end{align} $$对于切向畸变,用另外的参数纠正:
$$ \begin{align} x_\text{distorted}=x + 2p_1xy+p_2(r^2+2x^2)\\ y_\text{distorted}=x + 2p_2xy+p_1(r^2+2y^2) \end{align} $$- 三维空间归一化坐标为$[x,y]^T$
- 径向畸变和切向畸变
- 通过内参矩阵变换到像素平面
双目相机模型
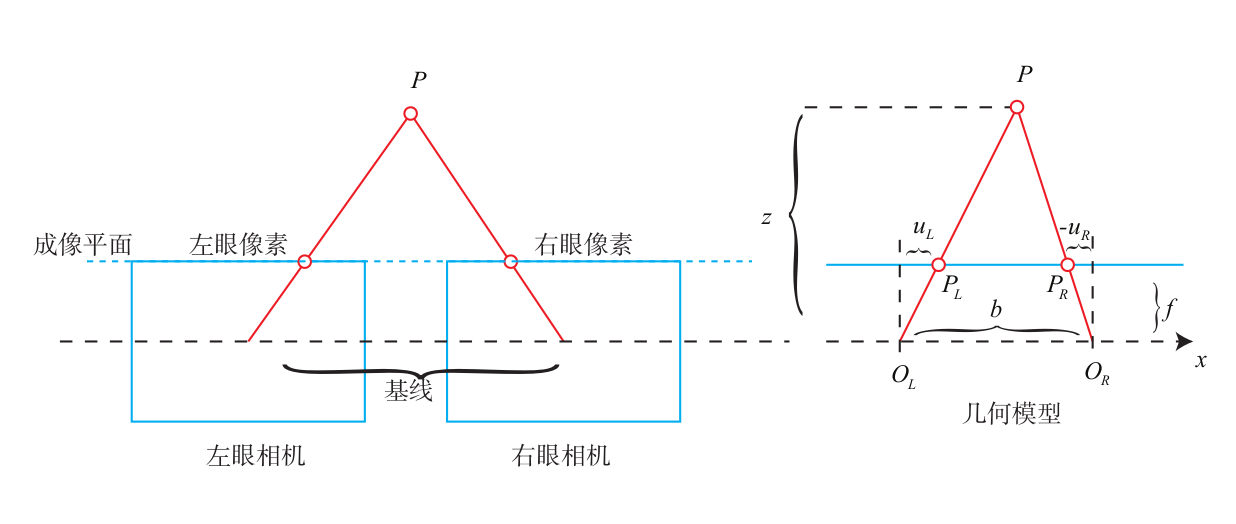 $$
\frac{z-f}{z}=\frac{b-u_L+u_R}{b}
$$
$$
z=\frac{fb}{d},\quad d\triangleq u_L-u_R
$$
$$
\frac{z-f}{z}=\frac{b-u_L+u_R}{b}
$$
$$
z=\frac{fb}{d},\quad d\triangleq u_L-u_R
$$$d$为视差,成像物体在中间,所以两边图像要看上去一样其中一张需要水平翻转,同一物体在两张图片中的横坐标差值(左右相机横放),视差越大距离越近,基线大的测得的最大距离越远,小的能够测量近处距离
RGB-D相机模型
-
红外结构光
-
飞行时间法(Time-of-flight,ToF)
实例
图像去畸变
opencv自带cv::Undistort()
每个点用公式计算一遍,颜色换算过去,但是要保证每个像素都有颜色,就必须使用去畸变后的每个图像位置去映射之前的图像中的像素
image_undistort.at<uchar>(v, u) = image.at<uchar>((int) v_distorted, (int) u_distorted);双目视觉
cv::StereoSGBM把左右图转为深度图,然后根据深度信息和两张原图拉伸成立体点云
RGB-D
非线性优化
状态估计问题
批量状态估计与最大后验估计
运动方程和观测方程
$$ \begin{cases} x_k=f(x_{k-1},u_k)+w_k\\ z_{k,j}=h(y_i,x_k)+v_{k,j} \end{cases} $$$x_k$为相机位姿,用$\text{SE}(3)$描述
观测方程可以表示成:
$$ sz_{k,j}=K(R_ky_j+t_k) $$$K$为相机内参,$s$为像素点距离(物体到镜头),被观测的物体发生$R_k$旋转和$t_k$平移
假设噪声$w_k,v_{k,j}$满足零均值高斯分布
$$ w_k\sim\mathcal{N}(0,R_k),v_k\sim\mathcal{N}(0,Q_{k,j}) $$$\mathcal{N}$表示高斯分布,$0$表示零均值,$R_k,Q_{k,j}$表示协方差矩阵,在有噪声情况根据$z$和$u$推断位姿$x$和地图$y$,构成状态估计问题
两种方式:
- 用当前时刻估计来估计后来的数据,增量/渐进,滤波器,扩展卡尔曼滤波(EKF)
- 批量一次性处理数据
折中方法:滑动窗口估计
考虑从$1$到$N$的所有时刻,假设有$M$个路标点。所有时刻机器人位姿和路标为
$$ x=\{x_1,\ldots,x_N\},\quad y=\{y_1,\ldots,y_M\} $$用不带下标的$u$表示所有时刻输入,$z$表示所有时刻的观测数据,对机器人状态估计。已知输入数据$u$和观测数据$z$的条件下,求状态$x,y$的条件概率分布:
$$ P(x,y|z,u) $$当输入数据不变,变为重建三维空间结构的问题,$P(x,y|z)$,Structure from Motion(SfM)
根据贝叶斯法则:
$$ P(x,y|z,u)=\frac{P(z,u|x,y)P(x,y)}{P(z,u)}\propto \sideset{}{}{\underbrace{P(z,u|x,y)}}_{似然} \space \sideset{}{}{\underbrace{P(x,y)}}_{先验} $$未完
视觉里程计
特征点法
提取图像里面一些特别的地方
- 角点:Harris、FAST、GFTT
- 局部特征:SIFT、SURF、ORB(人工设计的特征点)
SIFT(尺度不变特征变换,Scale-Invariant Feature Transform)
ORB(Oriented FAST and Rotated BRIEF)
FAST关键点
- 选取像素$p$,假设亮度为$I_p$
- 设置阈值$T$(比如,$I_p$的20%)
- 以像素$p$为中心,选取半径为3的圆上16个像素点
- 假如选取的圆上有连续的$N$个点的亮度大于$I_p+T$或小于$I_p-T$,那么像素$p$可以被认为是特征点($N$ 通常取 12,即为 FAST-12。其他常用的$N$取值为 9 和 11,它们分别被称为 FAST-9 和 FAST-11)
- 循环以上四步,对每一个像素执行相同的操作
FAST-12算法更高效的排除不是角点的像素,在邻域圆上第1,5,9,13的像素,只有4个中有3个同时大于$I_p+T$或小于$I_p-T$,当前像素才有可能是角点
BRIEF描述子
特征匹配
- 暴力匹配
- 快速近似最临近(FLANN)
ORB特征
2D-2D:对极几何
对极约束
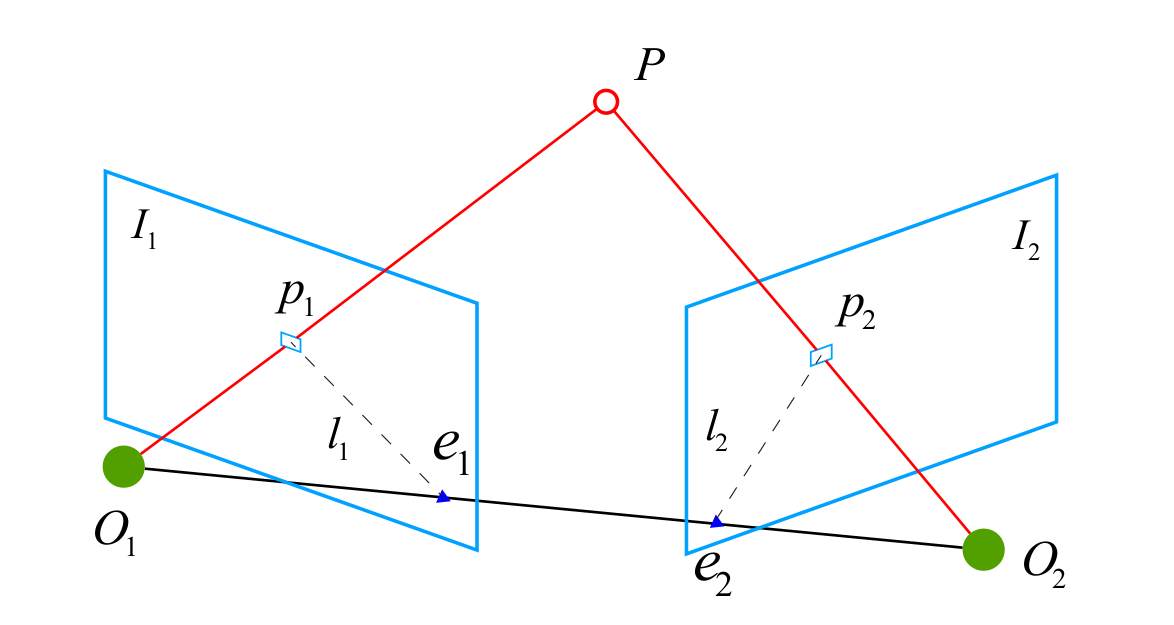
如果特征点匹配正确,$O_1,p_1,P,O_2,p_2$为同一平面上,称为极平面(Epipolar plane),和像平面的交点$e_1,e_2$称为极点(Epipoles),$O_1O_2$称为基线(Baseline),$l_1,l_2$为极线(Epipolar line)
$$ P=[X,Y,Z]^T $$两个像素点的位置为
$$ s_1p_1=KP,\quad s_2p_2=K(RP+t) $$$s_1p_1$和$p_1$构成投影关系,齐次坐标意义下是相等的,成为尺度意义下的相等
$$ sp\simeq p $$投影关系写作
$$ p_1\simeq KP,\quad p_2\simeq K(RP+t) $$取
$$ x_1=K^{-1}p_1,\quad x_2=K^{-1}p_2 $$带入上个公式
$$ x_2\simeq Rx_1+t $$两边左乘$t^\wedge$,相当于两边和$t$外积
$$ t^\wedge x_2 = t^\wedge Rx_1 $$两边左乘$x_2^T$
$$ x_2^Tt^\wedge x_2\simeq x_2^Tt^\wedge Rx_1 $$左边$t^\wedge x_2$是和$t$和$x_2$垂直的向量,再做内积得到0,
$$ x_2^Tt^\wedge Rx_1=0 $$代入$p_1,p_2$
$$ p_2^TK^{-T}t^\wedge RK^{-1}p_1=0 $$称为对极约束,几何意义为$O_1,P,O_2$三者共面,把中间部分记为两个矩阵:基础矩阵(Fundamental Matrix)$F$和本质矩阵(Essential Matrix)$E$,简化为
$$ E=t^\wedge R,\quad F=K^{-T}EK^{-1}, \quad x_2^TEx_1=p_2^TFp_1=0 $$位姿估计两步:
- 根据配对的像素点求出$E$或者$F$
- 根据$E$或者$F$求出$R,t$
本质矩阵
八点法求解$E$,$x_1=[u_1,v_1,1]^T,x_2=[u_2,v_2,1]^T$
$$ (u_2,v_2,1)\begin{pmatrix} e_1 & e_2 & e_3 \\ e_4 & e_5 & e_6 \\ e_7 & e_8 & e_9 \end{pmatrix}\begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} = 0 $$$$ u_2u_1e_1+u_2v_1e_2+u_2e_3+u_1v_2e_4+v_1v_2e_5+v_2e_6+u_1e_7+v_1e_8+e_9=0 $$$$ \left [u_2u_1,u_2v_1,u_2,u_1v_2,v_1v_2,v_2,u_1,v_1,1\right ]\cdot e=0 $$放到方程组里面
$$ \begin{pmatrix} u_2^2u_1^2&u_2^2v_1^2&u_2^2&u_1^2v_2^2&v_1^2v_2^2&v_2^2&u_1^2&v_1^2&1\\ u_2^2u_1^2&u_2^2v_1^2&u_2^2&u_1^2v_2^2&v_1^2v_2^2&v_2^2&u_1^2&v_1^2&1\\ \vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots&\vdots\\ u_2^8u_1^8&u_2^8v_1^8&u_2^8&u_1^8v_2^8&v_1^8v_2^8&v_2^8&u_1^8&v_1^8&1 \end{pmatrix} = \begin{pmatrix} e_1\\ e_2\\ e_3\\ e_4\\ e_5\\ e_6\\ e_7\\ e_8 \end{pmatrix} = 0 $$如果系数矩阵是满秩的(即秩为 8),那么它的零空间维数为 1
一个矩阵A的列秩是A的线性独立的纵列的极大数,通常表示为r(A),rk(A)或rank A,通常把满秩矩阵叫做可逆矩阵,det(A)≠0,不满秩的矩阵叫做奇异矩阵,det(A)=0
经过奇异值分解(SVD)
$$ E=U\Sigma V^T $$$U,V$为正交矩阵,$\Sigma$为奇异值矩阵
奇异值分解(SVD)https://zhuanlan.zhihu.com/p/29846048
根据$E$的内在性质,$\Sigma=\text{diag}(\sigma,\sigma,0)$,在 SVD分解中,对于任意一个 E,存在两个可能的 $t,R$ 与它对应:
$$ \begin{align} t_1^\wedge=UR_Z(\frac{\pi}{2})\Sigma U^T, \quad R_1=UR_Z^T(\frac{\pi}{2})V^T\\ t_2^\wedge=UR_Z(-\frac{\pi}{2})\Sigma U^T, \quad R_2=UR_Z^T(-\frac{\pi}{2})V^T \end{align} $$diag代表根据对角元素创建矩阵
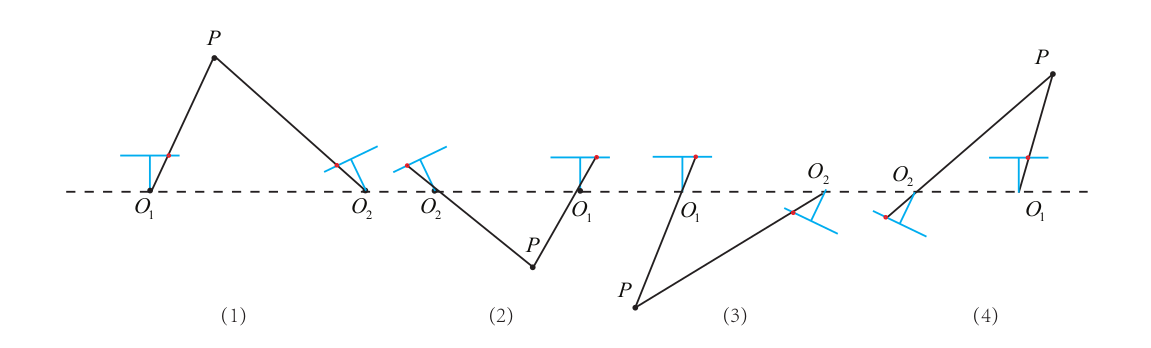
$R_Z(\frac{\pi}{2})$表示沿 $Z$ 轴旋转 $90\degree$ 得到的旋转矩阵。由于$-E$和$E$等价,所以对任意一$t$取负号得到同样结果,因此,从$E$分解到$t,R$时存在4个可能的解
单应矩阵
场景中的特征点都落在同一平面(比如墙壁和地面等),平面方程满足
$$ n^TP+d=0 $$$n$是平面法向量,$P$是世界坐标原点到P的向量,点积为负,加上原点到平面距离为0,整理后得到
$$ -\frac{n^TP}{d}=1 $$代入运动方程:
$$ s_1p_1=KP,\quad s_2p_2=K(RP+t) $$$$ \begin{align} p_2 &\simeq K(RP+t)\\ &\simeq K\left(RP+t\cdot\left(-\frac{n^TP}{d}\right)\right)\\ &\simeq K\left(R-\frac{tn^T}{d}\right)P\\ &\simeq K\left(R-\frac{tn^T}{d}\right)K^{-1}p_1 \end{align} $$得到$p_1$和$p_2$之间的变换,记作$H$
$$ p_2\simeq Hp_1 $$类似用矩阵元素方式表示
$$ \begin{pmatrix} u_2 \\ v_2 \\ 1 \end{pmatrix} = k\begin{pmatrix} h_1 & h_2 & h_3 \\ h_4 & h_5 & h_6 \\ h_7 & h_8 & h_9 \end{pmatrix}\begin{pmatrix} u_1 \\ v_1 \\ 1 \end{pmatrix} $$$$ \begin{align} u_2=k(h_1u_1+h_2v_1+h_3)\\ v_2=k(h_4u_1+h_5v_1+h_6)\\ 1=k(h_7u_1+h_8v_1+h_9)\\ \end{align} $$最后
$$ \begin{align} u_2=\frac{h_1u_1+h_2v_1+h_3}{h_7u_1+h_8v_1+h_9}\\ v_2=\frac{h_4u_1+h_5v_1+h_6}{h_7u_1+h_8v_1+h_9} \end{align} $$通常乘以非零因子使得$h_9=1$,整理得:
$$ \begin{align} h_1u_1+h_2v_1+h_3-h_7u_1u_2-h_8v_1u_2=u_2\\ h_4u_1+h_5v_1+h_6-h_7u_1v_2-h_8v_1v_2=v_2 \end{align} $$通过4对匹配特征点解线性方程组
$$ \begin{pmatrix} u_1^1 & v_1^1 & 1 & 0 & 0 & 0 & -u_1^1u_2^1 & -v_1^1u_2^1\\ 0 & 0 & 0 & u_1^1 & v_1^1 & 1 & -u_1^1v_2^1 & -v_1^1v_2^1\\ u_1^2 & v_1^2 & 1 & 0 & 0 & 0 & -u_1^2u_2^2 & -v_1^2u_2^2\\ 0 & 0 & 0 & u_1^2 & v_1^2 & 1 & -u_1^2v_2^2 & -v_1^2v_2^2\\ u_1^3 & v_1^3 & 1 & 0 & 0 & 0 & -u_1^3u_2^3 & -v_1^3u_2^3\\ 0 & 0 & 0 & u_1^3 & v_1^3 & 1 & -u_1^3v_2^3 & -v_1^3v_2^3\\ u_1^4 & v_1^4 & 1 & 0 & 0 & 0 & -u_1^4u_2^4 & -v_1^4u_2^4\\ 0 & 0 & 0 & u_1^4 & v_1^4 & 1 & -u_1^4v_2^4 & -v_1^4v_2^4 \end{pmatrix}\begin{pmatrix} h_1\\ h_2\\ h_3\\ h_4\\ h_5\\ h_6\\ h_7\\ h_8\\ \end{pmatrix}= \begin{pmatrix} u_2^1\\ v_2^1\\ u_2^2\\ v_2^2\\ u_2^3\\ v_2^3\\ u_2^4\\ v_2^4 \end{pmatrix} $$