概率
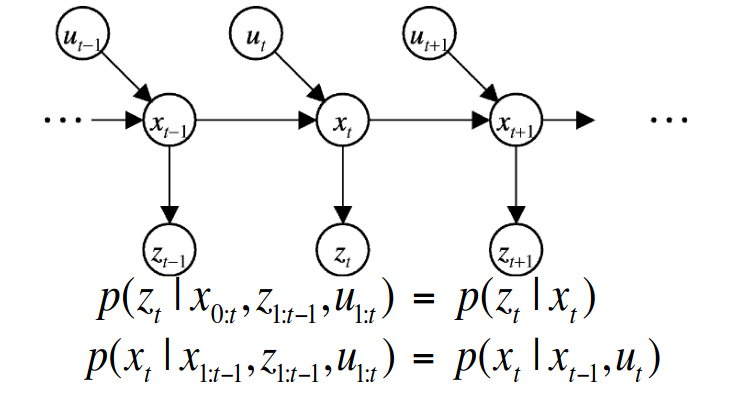
假设测量数据用\(\boldsymbol{z}_t\)表示,控制数据用\(\boldsymbol{u}_t\)表示,状态数据用\(\boldsymbol{x}_t\)表示状态
机器人的先验概率为:
\[ \overline{\text{bel}}(\boldsymbol{x}_t)=p(\boldsymbol{x}_t|\boldsymbol{z}_{1:t-1},\boldsymbol{u}_{1:t}) \]
后验概率为:
\[ \text{bel}(\boldsymbol{x}_t)=p(\boldsymbol{x}_t|\boldsymbol{z}_{1:t},\boldsymbol{u}_{1:t}) \]
其中\(\boldsymbol{z}_{1:t}\)代表从\(1\)到\(t\)时刻的测量
通常第一个概率称为预测,第二个概率称为修正或测量更新
对于概率来说,连续情况下计算:
\[ P(x|u)=\int P(x|u,x')P(x')dx' \]
离散情况下计算:
\[ P(x|u)=\sum P(x|u,x')P(x') \]
贝叶斯法则
\[ \begin{align} P(x|z)&=\frac{P(z|x)P(x)}{P(z)}\longrightarrow 后验概率=\frac{似然值 \cdot 先验概率}{证据} \\ &=\frac{P(z|x)P(x)}{P(x)P(z|x)+P(\overline{x})P(z|\overline{x})} \end{align} \]
例子
P(x)=0.01/100; // 携带HIV概率
P(~x)=1-P(x)=99.99/100 //不携带HIV概率
P(z|x)=99.9/100; // 携带HIV条件下测出阳性的概率
P(z|~x)=0.01/100; // 不携带HIV条件下测出阳性的概率
P(x|z)=P(x)P(z|x)/(P(x)P(z|x)+P(~x)P(z|~x))=0.01*99.9/(0.01*99.9+99.99*0.01)=0.5 // 检测到阳性真的携带HIV的概率贝叶斯滤波框架
给定:
- 测量数据集\(z\)和动作(控制)数据集\(u\)
\[ d_t=\{u_1,z_1,\cdots,u_t,z_t\} \]
- 传感器模型\(P(z|x)\)
- 控制模型\(P(x|u,x')\),\(x'\)代表上一次状态
- 系统状态先验概率\(P(x)\)
得到:
- 动态系统的估计状态\(x\)
- 状态的后验概率也被称为Belief(信念)
\[ \text{bel}(x_t)=P(x_t|u_1,z_1,\cdots,u_1,z_1) \]
马尔可夫假设
基本假设
- 静态世界
- 独立噪声
- 完美的模型,没有近似误差
贝叶斯滤波
全概率公式:
\[ P(B)=P(B|A)P(A)+P(B|\overline{A})P(\overline{A}) \]
推导贝叶斯滤波公式:
\[ \begin{align} \text{bel}(x_t)&=P(x_t|u_{1:t},z_{1:t})\\ &=\eta P(z_t|x_t,z_{1:t-1},u_{1:t})P(x_t|z_{1:t-1},u_{1:t}) \quad 贝叶斯\\ &=\eta P(z_t|x_t)P(x_t|z_{1:t-1},u_{1:t}) \quad 马尔可夫 \\ &=\eta P(z_t|x_t)\int P(x_t|x_{1:t-1},u_{1:t},z_{1:t-1})P(x_{t-1}|u_{1:t},z_{1:t-1})dx_{t-1} \quad 全概率公式 \\ &=\eta P(z_t|x_t)\int P(x_t|x_{t-1},u_{t})P(x_{t-1}|u_{1:t},z_{1:t-1})dx_{t-1} \quad 马尔可夫 \\ &=\eta P(z_t|x_t)\int P(x_t|x_{t-1},u_{t})P(x_{t-1}|u_{1:t-1},z_{1:t-1})dx_{t-1} \quad 马尔可夫,u_{t}不影响x_{t-1} \\ &=\eta P(z_t|x_t)\int P(x_t|x_{t-1},u_{t})\text{bel}(x_{t-1})dx_{t-1} \end{align} \]
\(P(x_t|x_{t-1},u_t)\)为状态转移概率,\(P(z_t|x_t)\)为测量概率
算法
\[ \begin{align} &\text{bayes\_filter}(\space\text{bel}(x), d\space): \\ &\hspace{4ex}\eta=0 \\ &\hspace{4ex}如果\space d\space为感知数据\space z\space, 那么 \\ &\hspace{8ex}对于所有\space x \\ &\hspace{12ex}\overline{\text{bel}}(x)=P(z|x)\text{bel}(x)\\ &\hspace{12ex}\eta=\eta+\overline{\text{bel}}(x)\\ &\hspace{8ex}对于所有\space x \\ &\hspace{12ex}\overline{\text{bel}}(x)=\eta^{-1}\overline{\text{bel}}(x)\\ &\hspace{4ex}否则如果\space d \space 为控制数据\space u \space,那么 \\ &\hspace{8ex}对于所有\space x \\ &\hspace{12ex}\overline{\text{bel}}(x)=\int P(x|u,x')\text{bel}(x')dx' \\ &\hspace{4ex}返回 \space \overline{\text{bel}}(x) \end{align} \]
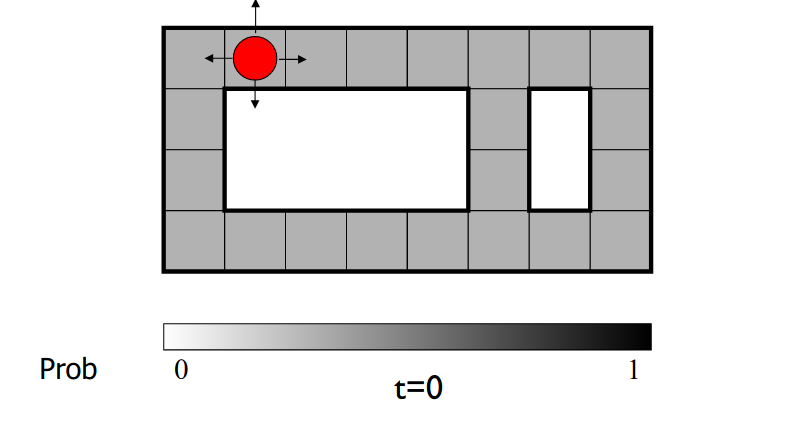
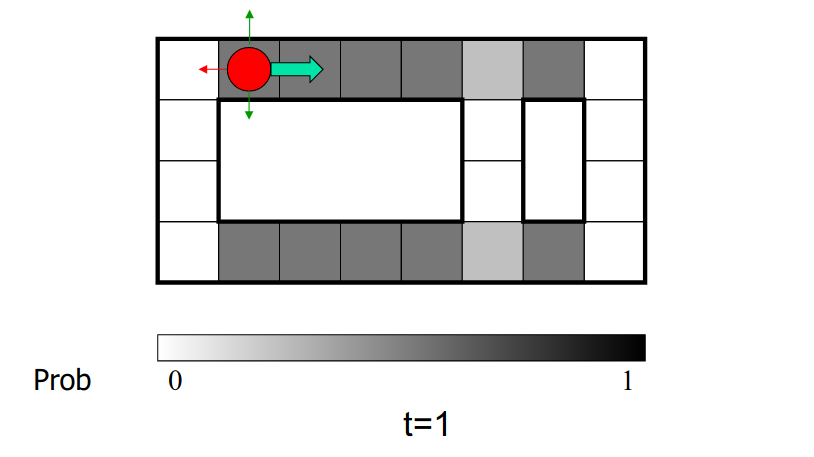
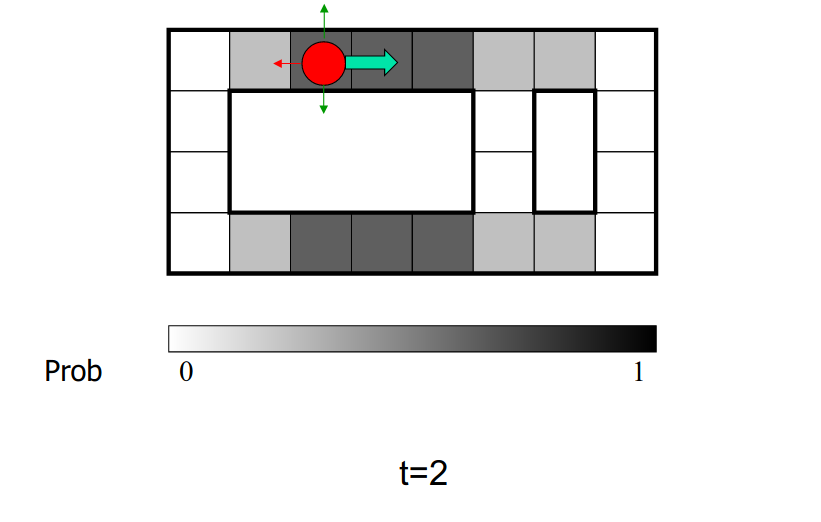
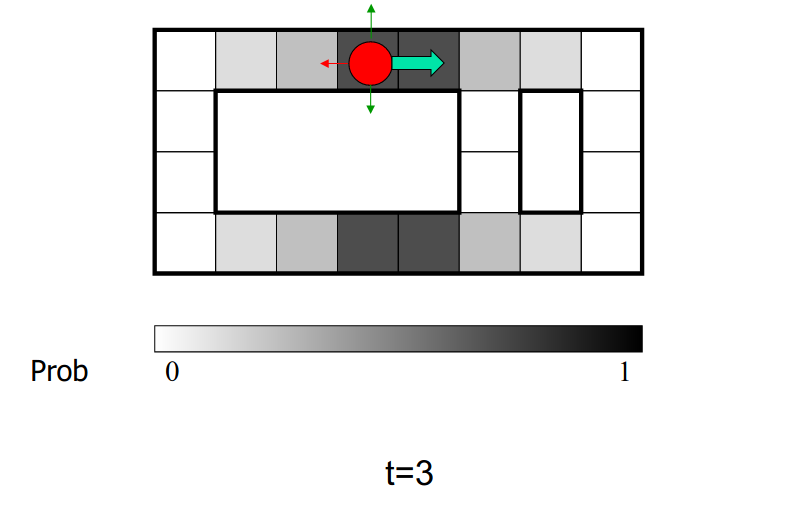
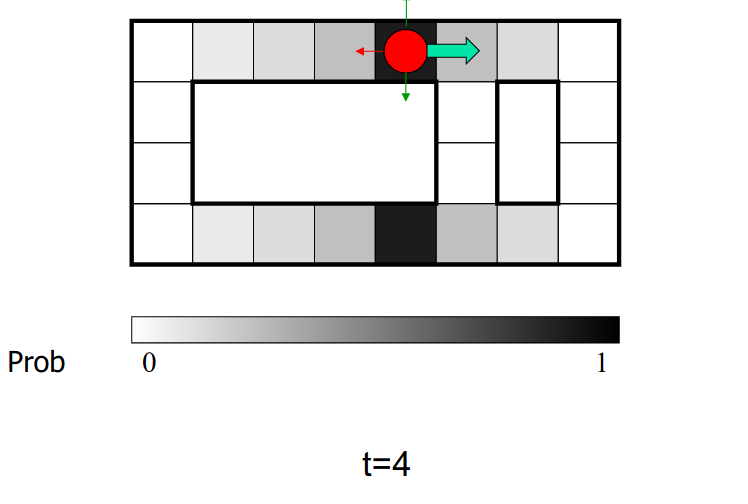
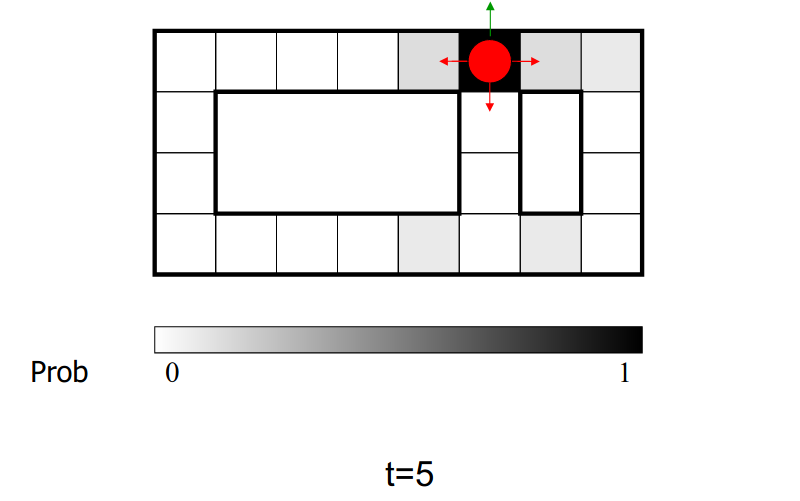
例子:机器人定位
传感器模型:能够知道四个方向是否有墙壁
运动模型:小概率的地方不会去
颜色越深的地方概率越大
参考
《概率机器人》
https://zhuanlan.zhihu.com/p/75380549
https://people.eecs.berkeley.edu/~pabbeel/cs287-fa13/slides/bayes-filters.pdf