《TARE: A Hierarchical Framework for Efficiently Exploring Complex 3D Environments via Smoothing and Mapping》
论文网站:https://www.cmu-exploration.com/tare-planner
相关工作
Frontier-based Exploration(基于前沿探索):已经建图区域和没有建图区域的边界。探索的时候,机器人朝着前沿走,不断扩展已经建图区域知道整个环境已经被探索。虽然这些方法中的大多数都贪婪地选择边界进行探索,但Faigl和Kulich的方法通过解决画廊问题的变体来确定覆盖边界的最小视点集。类似地,我们的方法也找到最小视点集,但通过递归和随机采样视点来实现。
Topological Exploration(拓扑探索):大多数这些方法将环境划分为拓扑上不同的部分,通过对这些部分进行详尽的遍历来完全探索整个环境。虽然这些方法注重拓扑的完整性,但我们的方法旨在生成环境的详细地图。
Random Sampling-based Methods(基于随机抽样的方法):最近的研究工作开发了一些基于快速探索随机树(Rapidly-exploring Random Tree,RRT)的方法或快速探索随机图(Rapidly-exploring Random Graph,RRG)。使用该方法的有:
- Next-Best-View Planner(NBVP)
- Graph-Based exploration Planner(GBP)
- Motion primitives-Based exploration Planner(MBP)
问题定义
定义 \(\mathcal{Q}\subset \mathbb{R}^3\) 为需要探索的工作空间。让 \(\mathcal{Q}_{\text{trav}}\subset \mathcal{Q}\) 为可遍历的子空间。定义视点 \(\mathbf{v}\in\mathbf{SE}(3)\) 来描述机器人搭载的传感器位姿,其中 \(\mathbf{p_v}\in\mathcal{Q_{\text{trav}}}\) 和 \(\mathbf{q_v}\in\mathbf{SE(3)}\) 分别表示位置和方向。用 \(\mathcal{L}\subset \mathbf{SE(3)}\) 表示沿车辆过去轨迹的视点集。我们使用术语“表面(surface)”来指代自由空间和非自由空间之间的广义边界,后者包括占据的空间和未知的空间。使 \(\mathcal{S_{\text{v}}}\subset \mathcal{Q}\) 为传感器在 \(\mathbf{v}\) 时刻感知到的表面。相同的表面在不同的视点可以被感知到。到目前为止感知到的表面为
\[ \mathcal{S} = \bigcup_{\mathbf{v}\in \mathcal{L}}{\mathcal{S}_{\text{v}}}. \]
这里, \(\mathcal{S}\) 包含被覆盖的表面,表示为 \(\mathcal{S}_{\text{cov}}\subset \mathcal{S}\) ,未被覆盖的表面,表示为 \(\bar{\mathcal{S}}=\mathcal{S}\setminus \mathcal{S}_{\text{cov}}\) 。我们希望找到一条最短路径,当车辆按照该路径行驶时,能够覆盖整个表面 \(\bar{\mathcal{S}}\) 。路径必须满足运动动力学约束。让 \(\mathbf{v}_{\text{current}}\) 作为在当前传感器位姿定位下的视点。问题定义为如下
问题1:给定 \(\bar{\mathcal{S}}\) 和 \(\mathbf{v}_{\text{current}}\) ,寻找最短的由当被车辆覆盖 \(\bar{\mathcal{S}}\) 跟踪的视点 \(\mathbf{v}_1,\mathbf{v}_2,\dots\) 形成路径 \(\mathcal{T}^*\) , 在 \(\mathbf{v}_{\text{current}}\in\mathcal{T}^*\) 下, \(\mathcal{T}^*\) 为动力学合适的。
问题 1 在每个规划周期重复解决。我们使用 \(\bar{\mathcal{S}}\) 来计算探索路径。当执行路径,我们使用最新的传感器数据更新 \(\bar{\mathcal{S}}\) ,计算被取代的和新感知的表面。然后,我们将表面从 \(\bar{\mathcal{S}}\) 变为 \(\mathcal{S}_{\text{cov}}\),并在下一个规划周期中使用 \(\bar{\mathcal{S}}\),因此探索将继续进行。
方法
A. 视点采样
我们定义了传感器覆盖表面点的标准。考虑以 \(\mathbf{p}_s\in \mathcal{Q}\) 为中心且法线 \(\mathbf{n}_s \in \mathbb{R}^3\) 朝向未知空间(free-space)的一侧的表面区域,在表面区域的中心点被视点 \(\mathbf{v}\) 覆盖,如果
\[ \begin{gather} |\mathbf{p}_{\mathcal{s}}-\mathbf{p}_\mathbf{v}| \le D, \\ \mathbf{n}_{\mathcal{s}} \cdot (\mathbf{p}_\mathbf{v}-\mathbf{p}_{\mathcal{s}})/|\mathbf{n}_{\mathcal{s}}||\mathbf{p}_\mathbf{v}-\mathbf{p}_{\mathcal{s}}|\ge T, \end{gather} \]
其中 \(D\) 和 \(T\) 为两个与视点有关的常数,约束表面区域的相对距离和方向。这些标准激励下使得可以很好地感知表面。实践中, \(D\) 设置得比传感器范围要小。
定义 \(\mathcal{H}\subset \mathcal{Q}\) 为如图2所示的局部路径规划区间。使 \(\mathcal{H}_{\text{trav}}\subset \mathcal{H}\) 为可遍历(traversable)的通过考虑碰撞和连通性进行识别的子空间,同时使 \(\mathcal{C}_{\text{trav}}^{\mathcal{H}}\) 为考虑旋转和平移的相应配置空间。定义 \(\bar{\mathcal{S}_{\mathcal{H}}} \subset \bar{\mathcal{S}}\) 为可以从 \(\mathcal{C}_{\text{trav}}^{\mathcal{H}}\) 中的视点被感知的未被覆盖的表面。视点采样的问题为在 \(\mathcal{C}_{\text{trav}}^{\mathcal{H}}\) 中选择一个最小的视点集合覆盖 \(\bar{\mathcal{S}}_\mathcal{H}\) 。让我们用 \(\bar{\mathcal{S}_\mathbf{v}}\subset \bar{\mathcal{S}_\mathcal{H}}\) 表示要从 \(\mathbf{v}\in\mathcal{C}_{\text{trav}}^\mathcal{H}\) 中感知的未覆盖表面。 \(\mathbf{v}\)的奖励定义为 \(\bar{\mathcal{S}}_{\mathbf{v}}\) 的区域,表示为 \(A_{\mathbf{v}}\) 。
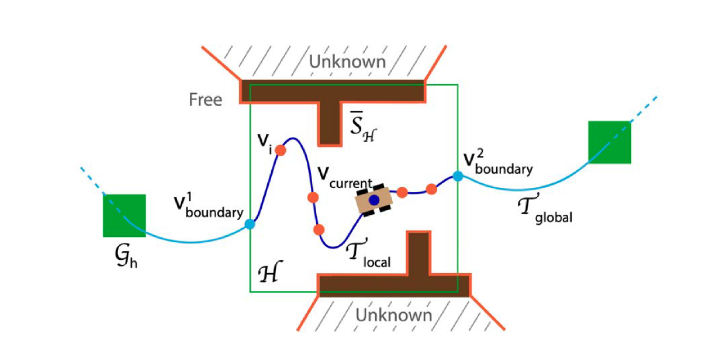 图2
图2
数学定义插图。绿色方框代表局部路径规划范围 \(\mathcal{H}\) 。实心绿色方块代表探索子空间 \(\mathcal{G}_{h}\), \(h\in \mathbb{Z}^+\)。深蓝色曲线为局部路径 \(\mathcal{T}_{\text{local}}\) 。 \(\mathcal{T}_{\text{local}}\) 上的深蓝色点为当前视点 \(\mathbf{v}_\text{current}\) 。浅蓝色的点为视点 \(\mathbf{v}^1_{\text{boundary}}\) 和 \(\mathbf{v}^2_{\text{boundary}}\) 在 \(\mathcal{H}\) 的边界上, \(\mathcal{T}_{\text{local}}\) 和 \(\mathcal{T}_{\text{global}}\) 相连。 橙色的点为采样的视点 \(\mathbf{v}_i,i\in\mathbb{Z}^+\) 。橙色的线条为未覆盖的表面 \(\bar{\mathcal{S}}_\mathcal{H}\) 等待被视点感知。该方法使用迭代随机抽样过程来确定 \(\mathbf{v}_i\) 覆盖 \(\bar{\mathcal{S}}_\mathcal{H}\) 。
请注意,该问题表现出子模块化,例如,选择的视点越多,选择额外视点的奖励就会减少。这是因为邻近视点具有重叠的视场,并且可以从多个视点感知相同的表面。因此,视点的奖励取决于之前选择的视点。设 \(\mathbf{v}_i, i\in \mathbb{Z}^+\) ,为第 \(i\) 个选择的视点。从 \(\mathbf{v}_i,\bar{\mathcal{S}}_{\mathbf{v}_i}\) 中感知的表面需要调整为 \(\bar{\mathcal{S}}_{\mathbf{v}_i}-\bigcup^{i-1}_{j=1}\left( \bar{\mathcal{S}}_{\mathbf{v}_i} \cap \bar{\mathcal{S}}_{\mathbf{v}_j} \right)\) 。然后 \(A_{\mathbf{v}_i}\) 相应的进行调整。
算法1展现了视点采样的过程。
- 第1行:从 \(\mathcal{H}_{\text{trav}}\) 里的格子(lattice pattern)中生成一系列的均匀的预选视点 \(\mathcal{V}\)
- 第3行:通过估计预选视点 \(\mathbf{v}\in \mathcal{V}\) 的覆盖使用更新的环境表示形式的 \(\bar{\mathcal{S}}_{\mathbf{v}}\) 计算奖励 \(A_{\mathbf{v}}\)
- 第6-11行:在每次迭代中,算法从 \(\mathcal{V}\) 中随机采样覆盖 \(\bar{\mathcal{S}}_\mathcal{H}\) 的视点子集,预先选择三个视点,一个是当前视点 \(\mathbf{v}_{\text{current}}\) ,其他两个是边界视点 \(\mathbf{v}_{\text{boundary}}^1,\mathbf{v}_{\text{boundary}}^2\) ,把全局路径和局部路径连接起来。决定怎样得到 \(\mathbf{v}_{\text{boundary}}^1,\mathbf{v}_{\text{boundary}}^2\) 的过程在后面有讲解
- 第8行:优先级队列 \(\mathcal{Q}'\) 用于管理候选视点。 视点 \(\mathbf{v}\) 的优先级设置为其奖励 \(A_{\mathbf{v}}\) 。 从优先级队列中选择观点,其概率与其奖励成正比
- 第10行:由于子模块性(thesubmodularity),在选择一个视点后,考虑到重叠的视场,优先级队列中剩余视点的奖励会相应减少
- 第12行:当优先级队列为空或者添加新视点的边际奖励可以忽略不计时,视点采样过程结束。 该算法调用算法2来生成通过采样视点的路径
\[ \begin{aligned} \hline \\ &\large{\textbf{算法1}:计算局部路径} \\ \hline \\ &\textbf{输入:} 可遍历的C-空间 \mathcal{C}_{\text{trav}}^{\mathcal{H}} ,未覆盖的表面 \bar{\mathcal{S}}_\mathcal{H} ,当前视点 \mathbf{v}_\text{current},边缘视点 \mathbf{v}^1_{\text{boundary}} 和 \mathbf{v}^2_{\text{boundary}} \\ &\textbf{输出:} 局部路径 \mathcal{T}_{\text{local}} \\ 1\ \ &在 \mathcal{C}_{\text{trav}}^{\mathcal{H}} 中生成视点集合 \mathcal{V} \\ 2\ \ &初始化优先队列 Q \\ 3\ \ &对于每个 \mathbf{v} \in \mathcal{V},估计覆盖率 \bar{\mathcal{S}}_{\mathbf{v}} ,然后把 \mathbf{v} 以奖励 A_{\mathbf{v}} 推入优先队列 Q \\ 4\ \ &\mathcal{T}_{\text{local}} \gets ∅,\ c_{best} \gets +\infty \\ 5\ \ &\mathbf{for}\ i:=1\ \text{to}\ K\ \mathbf{do} \\ 6\ \ &\quad Q'\gets Q,\mathcal{V}' \gets \{\mathbf{v}_{\text{current}}, \mathbf{v}_{\text{boundary}}^1,\mathbf{v}_{\text{boundary}}^2,\} \\ 7\ \ &\quad \textbf{while}\ Q'\ne \mathnormal{∅} \ \text{and} \ Q' 包含至少一个非零优先级\ \textbf{do} \\ 8\ \ &\quad\quad在Q'中概率选择视点\mathbf{v}',然后从Q'中移除\mathbf{v}' \\ 9\ \ &\quad\quad \mathcal{V}'\gets \mathcal{V}'\cup \mathbf{v}'; \\ 10\ \ &\quad\quad 在Q'中更新所有视点的优先级 \\ 11\ \ &\quad\textbf{end} \\ 12\ \ &\quad 使用算法2计算\mathcal{T}'_{\text{smooth}}和c'_{\text{smooth}} \\ 13\ \ &\quad \textbf{if} \ c'_{\text{smooth}} <c_{\text{best}}\ \textbf{then} \\ 14\ \ &\quad\quad \mathcal{T}_{\text{local}}\gets\mathcal{T}_{\text{smooth}}',c_{\text{best}}\gets c'_{\text{smooth}}; \\ 15\ \ &\quad\textbf{end} \\ 16\ \ &\textbf{end} \\ 17\ \ &\textbf{return}\ \mathcal{T}_{\text{local}}; \\ \hline \end{aligned} \]
B. 路径生成和平滑
给定一个采样过的视点集合 \(\mathcal{V}'\) ,我们想生成一条通过每个视点的路径。理想情况下,我们希望路径符合动力学,可以让车辆以较高的速度跟踪。在这里,我们关注的曲率约束例如路径的最大曲率由车辆的最小转弯半径决定。由于 \(\mathcal{V}'\) 中视点的分布和环境中的结构,满足曲率约束的连续路径是不可能的。 该方法计算平滑路段的路径,如图3所示。车辆在每个路段的末端停下来,然后以不同的方向移动到下一个路段。 这就要求车辆能够在一处转弯。 考虑到本文的重点不是使用复杂的运动模型进行路径规划,我们采用通用的微分运动模型,并且对于飞行器而言,具有独立的高度控制。让我们定义路径为 \(\mathcal{T}'_{\text{smooth}}=[\mathbf{v}_1^1,\mathbf{v}_2^1,\cdots][\mathbf{v}_1^2,\mathbf{v}_2^2,\cdots]\cdots,\) 其中 \([\cdot]\) 代表一个路段同时 \(\mathbf{v}_k^j\) 为第 \(j\) 条路段上的第 \(k\) 个视点, \(j,k\in\mathbb{Z}^+\) 。请注意,路段上的最后一个视点和下一个路段上的第一个视点共享相同的视点。令 \(\tilde{n}\in\mathbb{Z}^+\) 为路段的数量, \(\tilde{n}\ge j\) 。定义 \(l_j\) 为第 \(j\) 条路段的长度。 我们通过在每次停止时应用惩罚 \(p\) 来阻止过于频繁地停止。 \(\mathcal{T}_\text{smooth}'\) 的代价定义为
\[ c_\text{smooth}'=\sum_{j=1}^{\tilde{n}}l_j+p(\tilde{n}-1) \]
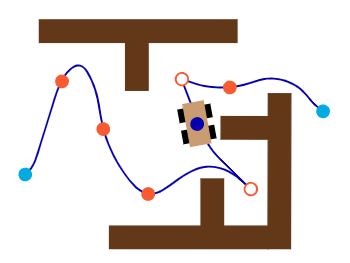
图3。平滑路径 \(\mathcal{T}_\text{smooth}\) 的图示。深蓝色曲线表示满足曲率约束的路径段。深蓝色的点是 \(\mathbf{v}_\text{current}\) 。浅蓝色的点为连接到 \(\mathcal{T}_\text{global}\) 的 \(\mathbf{v}_\text{boundary}^1\) 和 \(\mathbf{v}_\text{boundary}^2\) 。橙色点是采样视点,中空橙色点是路径段之间的断点。 车辆在每个断点处停下来,然后继续行驶到下一个路径段。
计算路径的问题可以表述如下。
问题2:给定视点 \(\mathcal{V}'\) ,寻找一条路径 \(\mathcal{T}_\text{smooth}^*=[\mathbf{v}_1^1,\mathbf{v}_2^1,\cdots][\mathbf{v}_1^2,\mathbf{v}_2^2,\cdots]\cdots\) 具有最低的 \(c_\text{smooth}'\) ,使得 \(\mathcal{T}_\text{smooth}'\) 访问 \(\mathcal{V}'\) 中的每个视点一次,并且 \(\mathcal{T}_\text{smooth}^*\) 上的每个路段都满足曲率约束。
问题2是NP难题,因为它是旅行商问题 (TSP) 的扩展版本。我们没有试图找到精确的解决方案,而是使用近似算法分两步解决问题。首先,我们使用标准TSP求解视点顺序。其次,我们按照顺序将视点分成路段。这是为了确定除了第一个和最后一个视点之外的视点是否是路段内的内点或两个路段之间的断点。令 \(n'\in \mathbb{Z}^+\) 为 \(\mathcal{V}′\) 中的视点数量。定义 \(\mathbf{x}=[x_1,x_2,\cdots,x_{n'-2}]\) 作为描述 \(n'−2\) 个视点(不包括第一个和最后一个)状态的布尔变量序列和一个函数 \(f(\mathbf{x})=c'_\text{smooth}\) 。确定视点状态的问题可以表述为
问题3:给定一个布尔变量序列 \(\mathbf{x}\) 和一个函数 \(f(\mathbf{x}) =c'_\text{smooth}\) ,找到 \(\mathbf{x}^*\) 使得
\[ \mathbf{x}^*=\text{argmin}_{\mathbf{x}}{c'_\text{smooth}} \]
问题3是一个非线性整数规划问题,被称为NP困难问题。特别是寻找平滑路径涉及耗时的轨迹优化。我们的方法没有使用具有较高计算复杂度的现有启发式方法,而是应用贪婪策略仅检查每个观点一次,从而最大限度地减少运行时间。
\[ \begin{aligned} \hline\\ &\large{\textbf{算法2}:从视点计算局部路径}\\ \hline\\ &\textbf{输入:} 可探索C空间 \mathcal{C}^\mathcal{H}_{\text{trav}},视点 \mathcal{V}' \\ &\textbf{输出:} 平滑的路径 \mathcal{T}'_\text{smooth} 和代价 c'_\text{smooth} \\ 1\ \ &计算\mathcal{V}'中视点对之间的最短路径,然后创建距离矩阵\mathbf{D}';\\ 2\ \ &使用 \mathbf{D}' 解决 \mathbf{TSP} 问题计算路径 \mathcal{T} ';\\ 3\ \ &使用 \mathcal{T}' 初始化 \mathcal{T}'_\text{smooth},然后在 \mathcal{T}_\text{smooth} 上设置 视点 \mathbf{v}_2,\mathbf{v}_3,\cdots,\mathbf{v}_{n-1} 作为断点; \\ 4\ \ &平滑 \mathcal{T}'_\text{smooth} 上连续视点之间的路段并计算代价 c'_\text{smooth}; \\ 5\ \ &\textbf{for} \ i :=2\ \text{to}\ n'-1\ \textbf{do} \\ 6\ \ &\quad 通过连接 \mathbf{v}_i 两侧的两个线段,暂时将视点 \mathbf{v}_i 设置为内点(\text{inner-point}) \\ 7\ \ &\quad 通过 \mathbf{v}_i 平滑路径段,计算代价 c'_\text{temp} \\ 8\ \ &\quad \textbf{if} \ c'_\text{temp} < c'_\text{smooth}\ \text{and} \ \mathcal{T}'_\text{smooth} 符合曲率约束\ \textbf{then}\\ 9\ \ &\quad\quad 最终确定 \mathcal{T}'_\text{smooth} 上的 \mathbf{v}_i 作为内点;\\ 10\ \ &\quad\quad c'_\text{smooth}\gets c'_\text{temp};\\ 11\ \ &\quad\textbf{end}\\ 12\ \ &\textbf{end}\\ 13\ \ &\textbf{return}\ \mathcal{T}'_\text{smooth},c'_\text{smooth};\\ \hline \end{aligned} \]
算法2给出了从一组视点 \(\mathcal{V}'\) 计算 \(\mathcal{T}'_\text{smooth}\) 的过程。
- 第1行: 该算法使用 \(\mathbf{A}^*\) 算法找到 \(\mathcal{V}'\) 中每个视点对之间的最短无碰撞路径,并构造包含路径长度的距离矩阵 \(\mathbf{D}'\) 。
- 第2行:接下来,该算法求解视点遍历顺序的TSP。
- 第3行:在确定 \(\mathcal{T}'_\text{smooth}\) 上的线段后,算法将所有 \(n'−2\) 个视点初始化为断点。
- 第4行:并平滑连续视点之间的线段。
- 第5-11行:随后,该算法尝试通过内点顺序设置每个视点并通过 \(\mathbf{v}_i\) 重新平滑片段来降低代价 \(c'_\text{smooth}\) 。
每个路径段都使用类似于[30]的轨迹优化方法进行平滑,其中该段被建模为在视点处连接的一组三次样条线。边界条件应用于视点。样条曲线的控制点放置在 \(\mathbf{A}^*\) 搜索给出的初始路径上,并由非线性优化求解器[31]进行调整,以考虑碰撞间隙和路径平滑度。为了加速处理,非线性优化被边缘化,其中仅优化 \(\mathbf{v}_i\) 的两个相邻视点之间的样条。 该算法返回 \(\mathcal{T}'_\text{smooth}\) 和 \(c'_\text{smooth}\) 。
C. 全局规划
我们将 \(\mathcal{H}\) 之外的空间划分为均匀的长方体子空间。每个子空间存储在探索过程中开发的覆盖和未覆盖的表面。请注意,数据保留在子空间中仅用于存储,而 \(\mathcal{H}\) 中的数据会随着探索的进行而主动更新。每个子空间都具有“未探索”、“探索中”和“已探索”状态。 如果子空间不包含任何覆盖或未覆盖的表面,则状态为“未探索”。 如果子空间仅包含被覆盖的表面,则状态为“已探索”。 如果子空间包含任何未覆盖的表面,则状态为“探索中”。我们只考虑全局规划中的探索子空间。将 \(\mathcal{G}_h \subset \mathcal{Q},h \in \mathbb{Z}^+\) 表示为探索子空间,并将 \(\hat{\mathcal{G}}\) 表示为探索子空间的集合。全局规划问题是找到一条经过当前视点 \(\mathbf{v}_\text{current}\) 和 \(\hat{\mathcal{G}}\) 中各子空间质心的全局路径 \(\mathcal{T}_\text{global}\) 。在探索过程中,我们在从过去的轨迹扩展的可遍历空间中构建了一个稀疏随机路线图。与局部规划类似,我们在路线图上使用 \(\mathbf{A}^*\) 搜索来寻找子空间之间的最短路径,然后求解TSP。
\[ \begin{aligned} \hline\\ &\large{\textbf{算法3}:计算探索路径}\\ \hline\\ &\textbf{输入:}局部路径边界(horizon) \mathcal{H}, 可探索C空间 \mathcal{C}^{\mathcal{H}}_\text{trav},未覆盖表面 \bar{\mathcal{S}}_\mathcal{H},探索中子空间\hat{\mathcal{G}},当前视点\mathbf{v}_\text{current} \\ &\textbf{输出:}探索路径 \mathcal{T}\\ 1\ \ &计算\hat{\mathcal{G}}和\mathbf{v}_\text{current}中的质心之间的最短路径,然后创建距离矩阵\mathbf{D};\\ 2\ \ &通过使用\mathbf{D}求解\textbf{TSP}来计算全局路径 \mathcal{T}_\text{global};\\ 3\ \ &提取\mathbf{v}^1_\text{boundary}和\mathbf{v}^2_\text{boundary}作为\mathcal{T}_\text{global}与H边界的交集;\\ 4\ \ &使用算法1计算本地路径\mathcal{T}_\text{local};\\ 5\ \ &连接\mathcal{T}_\text{local}和\mathcal{T}_\text{global}生成\mathcal{T};\\ \hline \\ \end{aligned} \]
算法3给出了计算探索路径的总体过程。
- 第1行:构造一个距离矩阵,其中包含路线图上找到的路径的长度。
- 第2行:解TSP
- 第3行:提取 \(\mathcal{T}_\text{global}\) 上与H边界相交的两点作为 \(\mathbf{v}^1_\text{boundary}\) 和 \(\mathbf{v}^2_\text{boundary}\)
- 第4行:使用算法1计算 \(\mathcal{T}_\text{local}\)
- 第5行:\(\mathcal{T}_\text{local}\) 和 \(\mathcal{T}_\text{global}\) 通过将 \(\mathcal{H}\) 中的 \(\mathcal{T}_\text{global}\) 部分替换为 \(\mathcal{T}_\text{local}\) 来连接
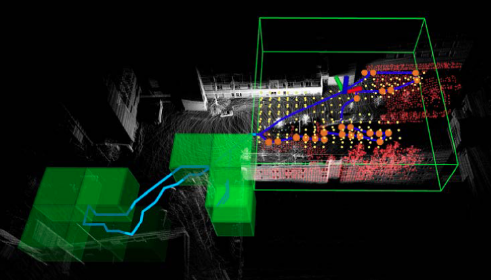
图4。使用真实数据的探索过程示例。该图使用与图2相同的颜色代码。白点显示激光雷达扫描数据,该方法使用该数据提取未覆盖的表面(红点)。黄点是候选视点,从中采样视点(橙色点)。
当在 \(\mathcal{H}(\bar{\mathcal{S}}_{\mathcal{H}}=∅)\) 中完成探索时,\(\mathcal{T}_\text{local}\) 减少为从 \(\mathbf{v}_\text{current}\) 连接到 \(\mathbf{v}^1_\text{boundary}\) 和 \(\mathbf{v}^2_\text{boundary}\) 的最短路径,这些路径进一步连接到 \(\mathcal{T}_\text{global}\) 上的相邻探索子空间。飞行器沿着路径传送到探索子空间以恢复探索。换句话说,该算法隐式地在探索和重新定位到另一个区域之间进行过渡以进一步探索。如果 \(\bar{\mathcal{S}}_{\mathcal{H}}=∅\) 且 \(\hat{\mathcal{G}}=∅\) ,则探索终止。
D. 理论分析
…