《Falco: Fast likelihood‐based collision avoidance with extension to human‐guided navigation》
介绍
采用分层方法把规划问题分为两个子问题,第一个问题解决的是全局规划问题,可能会辅以启发式方法,以确保路径不会陷入局部最小值。第二个问题是解决并行运行的局部规划问题,以跟踪全局路径并避开障碍物。在本文中,我们提出了一种可大大降低计算复杂度的方法,从而利用航空飞行器上的轻量级计算来确保安全飞行。
我们从概率的角度来制定规划问题。该方法并不寻求代价最低的路径(通常是最短路径),而是在确定下一步立即执行导航时,最大限度地提高到达目标的概率。
相关工作
搜索算法:
- 基于图搜索:Dijkstra,A*,D*
- 基于采样搜索:RRT和变种
- 基于地图:PRM(Probabilistic Roadmap),Voronoi graph,vector field
- 基于置信度: linear‐quadratic controller with Gaussian models,extend RRT with particles on each node to handlethe uncertainty of terrain friction,model the edge costs on a graph with uncertaintiesfor graph search.
问题定义
定义 \(Q\in\mathbb{R}\) 作为车辆的配置空间。使得 \(A\in Q\) 为车辆当前位置同时 \(B\in Q\) 为目标点。车辆上装了感知传感器。定义 \(S\in Q\) 作为传感器感知覆盖,也就是传感器范围。障碍在 \(S\) 中是确定的,在 \(Q \setminus S\) 中可能已知。考虑车辆有多个从 \(A\) 起步开始移动的方向。把当前起步状态定义为 \(x_S\) 。显然不同的 \(x_S\) 选择会导致不同路线。定义 \(P_B(\cdot)\) 为最有可能从给定状态成功到 \(B\) 的概率,和状态 \(x_S\) 关联的概率为 \(P_B(x_S)\) 。规划问题可以定义为:
问题1。给定 \(A,B\in Q,S\subset Q\) ,障碍在 \(Q\) 里面,计算 起始状态 \(x^*_S\) 来最大化概率 \(P_B(x_S)\) ,
\[ x_S^* = \arg \max_{x_S}{P_B(x_S)} \tag{1} \]
以上问题在车辆沿着路径运动每一步都会解,即在导航的每时每刻到达 \(B\) 的最大概率。
方法
概率模型
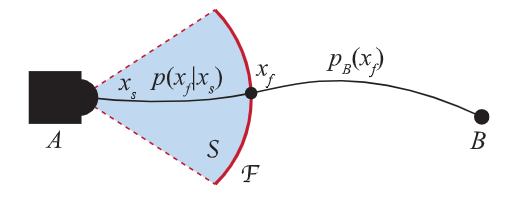
图2
\(\mathcal{F} \subset S\) 为传感器前沿
提出的方法最大化了从 \(A\) 行走到 \(B\) 的可能性。传感器范围 \(S\) 内的障碍可以通过传感器感知确切的得到。在 \(S\) 之外的如果有先验地图则可能知道。 \(S\) 需要根据车辆的运动模型展开,例如如果车辆可以横移。定义 \(x_f\) 为车辆穿过 \(\mathcal{F}\) 的时候的状态。 \(x_f\) 的条件分布为 \(x_x,p(x_f|x_S)\) ,能从感知传感器的障碍信息被推导出来。车辆从 \(x_f,P_B(x_f)\) 到达 \(B\) 点的概率密度能从先验地图的障碍中获得。我们有
\[ P_B(x_S) = \int P_B(x_f)p(x_f|x_S)\mathrm{d}x_f. \tag{2} \]
公式 \(P_B(x_S)\) 被重写为 \(P_B(x_S)\) 来表示概率密度。考虑 \(n\in \mathbb{Z}^+\) 次抽样 \(\xi_i, i = 1,2,\cdots,n\) ,摘自 \(p(x_f|x_S)\) 。根据蒙特卡洛抽样方法,我们可以得出
\[ \int P_B(x_f)p(x_f|x_S)\mathrm{d}x_f\approx_{n\uparrow\infty}\frac{1}{n}\sum_{i=1}^{n}{P_B(\xi_i)}. \tag{3} \]
结合以上两个公式,\(n\) 为常量:
\[ P_B(x_S)\approx\frac{1}{n}\sum_{i=1}^{n}{P_B(\xi_i)} \tag{4} \]
该公式表明在从 \(x_S,P_B(x_S)\) 导航到 \(B\) 时, 通过 \(n\gg1\) 次从条件分布 \(p(x_f|x_S)\) 中抽样,概率密度得到近似。需要注意的是通过抽样离散问题的方式给分布建模,使用有限的路径数量和体素可以解决该问题。
局部概率
给定起始状态 \(x_S\) ,车辆可以跟踪不同的路径达到传感器的前沿 \(\mathcal{F}\) 。把当前这一系列的路径同样叫做 \(x_S\) 。考虑一个 \(x_S\) 的离散模型。如图
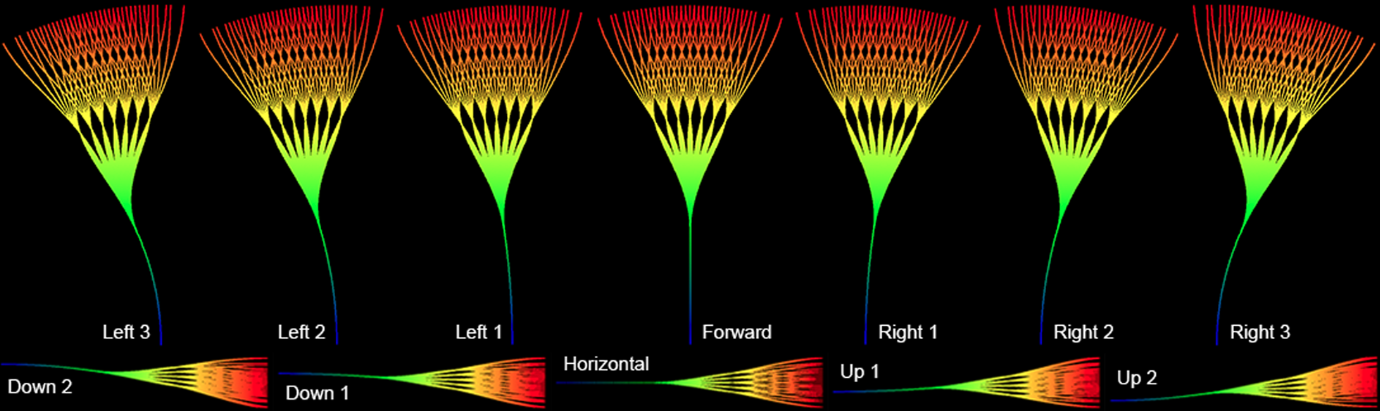
图3
最上面一行,有7组路径从上向下的视图呈现,其中 \(x_S\) 在路径起始曲线的左边或者右边。底下一行,有5组路径路径朝上或者朝下。考虑垂直和水平方向,例子中总共有 \(7\times 5=35\) 组路径。所有的路径都在 \(\mathcal{F}\) 结束。
每条路径都以三次样条曲线生成。路径在组里面被分为垂直和水平不同方向。图中,路径首先分割为35个方向(7水平和5垂直)同时每个又被分割为另外的35个方向。结果是每个组有 \(35^2=1225\) 条路径。考虑35个路径组,则总共有 \(35\times 1,225 = 42,875\) 条路径。图4显示了所有路径。
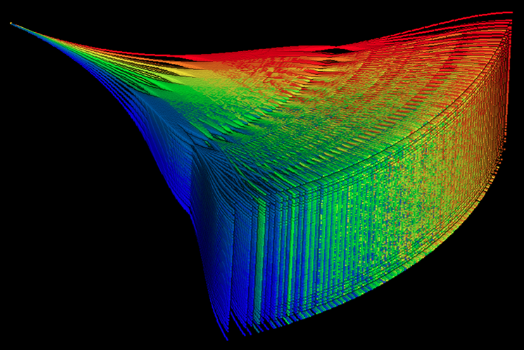
图4
路径组里面的路径都可以认为是从 \(x_S\) 到 \(\mathcal{F}\) 可行的。最后路径的状态可以被视为 \(x_f\) 的抽样 \(\xi_i, i = 1,2,\cdots,n\) ,其中分布是根据 \(p(x_f|x_S)\) 。导航期间,感知传感器检测到的障碍会和确定的路径发生碰撞。图5给出了组内避障后的无碰撞路线。定义一个Boolean函数 \(c(\xi_i)\) 来表示路径净空:
\[ c(\xi_i)=\begin{cases} 1,\quad \xi_i 不被包括,\\ 0,\quad 其他情况 \end{cases} \tag{5} \]
计算 \(P_B(x_S)\) 公式变为:
\[ P_B(x_S)\approx\frac{\sum^{n}_{i=1}c(\xi_i)P_B(\xi_i)}{\sum_{i=1}^{n}c(\xi_i)} \tag{6} \]
等式适用于所有路径组,并选择 \(P_B(x_S)\) 最高的路径组 \(x_S^*\) 供车辆执行。
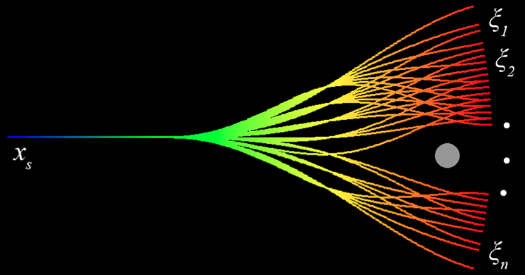
图5
全局概率
我们的环境用体素表示。与传统的体素表示法不同,我们的体素包含位置和方向信息。如图6a所示,一个体素根据一个恒定的角度间隔被分为多个方向,用 \(\delta\) 表示。定义 \(x_j^k,j,k\in\mathbb{Z}\) 为体素的状态,其中 \(j\) 为体素索引,\(k\) 为方向索引。与 \(x_j^k\) 相关的位置被模拟为在体素内均匀分布,方向被模拟为在 \(x_j^k\) 方向周围 \([-\delta/2, \delta/2]\) 内均匀分布。从 \(x_j^k\) 到达 \(B\) 的概率密度记为 \(P_B(x_j^k)\)。
概率可在相邻体素之间传递。如图6b所示,考虑概率从邻近体素传递到 \(x_j^k\) 的情况,表示为 左下的 \(j_l\) 和右上的 \(j_r\) 。让 \(\theta_k\) 为和 \(x_j^k\) 关联的方向。由于位置被建模为体素内的均匀分布,被转移到 \(x_j^k\) 的概率从 \(j_l\) 和 \(j_r\) 的相对的 \(1-\tan\theta_k/2\) 和 \(\tan\theta_k/2\) 个体素。在这里,灰色区域是通过在 \(j_l\) 和 \(j_r\) 中画一条与 \(x_j^k\) 方向平行的线,连接体素 \(j\) 的左下顶点和右上顶点来确定的。从每个灰色区域开始,概率从三个相邻的方向传输。概率密度传输定义为
\[ P_B(x_j^k)=\left(\left( 1-\frac{\tan\theta_k}{2} \right)\alpha + \frac{\tan\theta_k}{2}b \right)r_j \tag{7} \]
其中
\[ \begin{align} a = w_yP_B\left(x_{j_l}^{k-1}\right) + w_fP_B\left(x_{j_l}^{k}\right) + w_yP_B\left(x_{j_l}^{k+1}\right)\\ b = w_yP_B\left(x_{j_r}^{k-1}\right) + w_fP_B\left(x_{j_r}^{k}\right) + w_yP_B\left(x_{j_r}^{k+1}\right) \end{align} \]
\(r_j\) 代表由于障碍体素 \(j\) 的可穿越性,其中 \(r_j = 1\) 意思是完全净空, \(r_j=0\) 代表完全碰撞。 \(w_f\) 和 \(w_y\) 相对地决定了超前运动运动和yaw转向的可能的分布。我们规定
\[ w_f + 2w_y = 1 \tag{8} \]
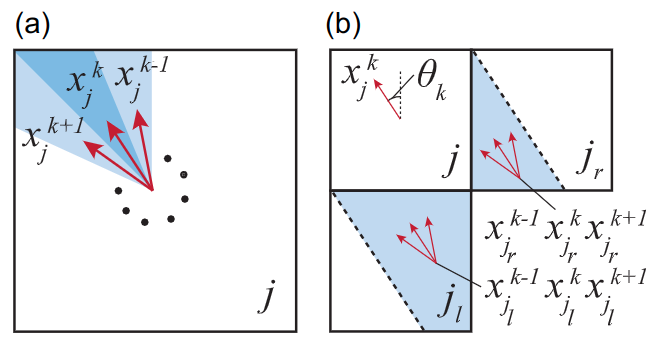
图6
三维情况是二维的扩展,在图6a中有多层,每层都和一个俯仰角关联。设 \(\alpha_l\) 为层的俯仰角 \(l,l\in\mathbb{Z}\) 。3D情况的体素状态为 \(x_j^{l,k}\) 。从邻近的体素概率密度的传输和2D是一样的。考虑俯仰角概率为
\[ P_B(x_j^{l,k}) = \left(\left( 1-\frac{|\tan\alpha_l|}{2}\left( \sin\theta_k + \cos\theta_k \right) \right) \left( \left ( 1-\frac{\tan\theta_k}{2} \right)c + \frac{\tan\theta_k}{2}d\right)+\frac{|\tan\alpha_l|}{2} \left( \sin\theta_k+\cos\theta_k\right)e\right)w_j^{l,k} \tag{9} \]
其中
\[ \begin{aligned} c = \space &w_{py}P_B\left(x_{jb}^{l-1,k-1}\right) + w_pP_B\left(x_{jb}^{l-1,k}\right) + w_{py}P_B\left(x_{jb}^{l-1,k+1}\right) \\ & + w_yP_B\left(x_{jb}^{l,k-1}\right) + w_fP_B\left(x_{jb}^{l,k}\right) + w_yP_B\left(x_{jb}^{l,k+1}\right) \\ & + w_{py}P_B\left(x_{jb}^{l+1,k-1}\right) + w_{p}P_B\left(x_{jb}^{l+1,k}\right) + w_{py}P_B\left(x_{jb}^{l+1,k+1}\right), \\ d = \space &w_{py}P_B\left(x_{jl}^{l-1,k-1}\right) + w_pP_B\left(x_{jl}^{l-1,k}\right) + w_{py}P_B\left(x_{jl}^{l-1,k+1}\right) \\ & + w_yP_B\left(x_{jl}^{l,k-1}\right) + w_fP_B\left(x_{jl}^{l,k}\right) + w_yP_B\left(x_{jl}^{l,k+1}\right) \\ & + w_{py}P_B\left(x_{jl}^{l+1,k-1}\right) + w_{p}P_B\left(x_{jl}^{l+1,k}\right) + w_{py}P_B\left(x_{jl}^{l+1,k+1}\right), \\ e = \space &w_{py}P_B\left(x_{jr}^{l-1,k-1}\right) + w_pP_B\left(x_{jr}^{l-1,k}\right) + w_{py}P_B\left(x_{jr}^{l-1,k+1}\right) \\ & + w_yP_B\left(x_{jr}^{l,k-1}\right) + w_fP_B\left(x_{jr}^{l,k}\right) + w_yP_B\left(x_{jr}^{l,k+1}\right) \\ & + w_{py}P_B\left(x_{jr}^{l+1,k-1}\right) + w_{p}P_B\left(x_{jr}^{l+1,k}\right) + w_{py}P_B\left(x_{jr}^{l+1,k+1}\right), \end{aligned} \]
这里,\(w_j^{lk}\) 表示 \(x_j^{lk}\) 因障碍物而产生的可穿越性。\(w_p\) 是与俯仰转弯相对应的权重,用于从 \(P_B(x_{j_*}^{l-1,k})\) 和 \(P_B(x_{j_*}^{l+1,k})\) 到 \(P_B(x^{l,k})\) 的概率传输,其中 \(*\) 代表 \(b,l\) 或 \(r\) 。 \(w_{py}\) 是与俯仰和偏航转向相对应的权重,用于 \(P_B(x_{j_*}^{l-1,k-1}),P_B(x_{j_*}^{l-1,k+1}),P_B(x_{j_*}^{l+1,k-1})和P_B(x_{j_*}^{l+1,k+1})\) 到 \(P_B(x^{l,k})\) 的概率传输。同样,我们要求在传输过程中没有概率损失,即
\[ w_f + 2w_p + 2w_y +4w_{pw}=1 \tag{10} \]
如果 \(\alpha_l<0\) ,则体素 \(j_b\) 将被体素 \(j\) 上方的体素(即体素 \(j_a\) )取代。有两种特殊情况。首先,如果 \(\alpha_l=0\) ,则车辆水平移动。在三维情况下,概率会从体素 \(j_l\) 和 \(j_r\) 传递到体素 \(j\) ,但不会从体素 \(j_a\) 或 \(j_b\) 传递到体素 \(j\) 。其次,如果 \(\theta_k=0\) ,车辆平行移动到体素 \(j_r\) 。在二维和三维情况下,概率从体素 \(j_l\) 而不是体素 \(j_r\) 传播到体素 \(j\) 。在初始化过程中,概率密度均匀分布在包含 \(B\) 的体素的所有方向上。图7给出了在二维环境中传播概率密度的示例。
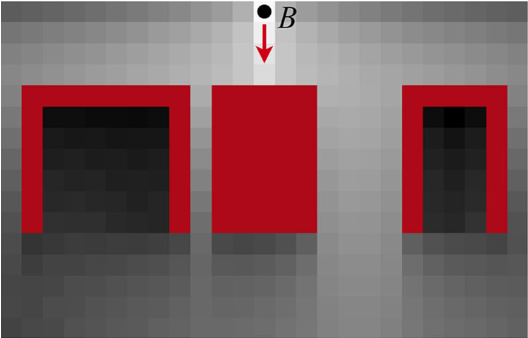
图7
方法实现
路径组是离线生成的。我们使用体素网格和传感器范围 \(S\) 来做碰撞检测。体素和路径之间的对应关系预先建立并存储在邻接列表中。在邻接列表中,每一行都与一个体素相关联,并由被位于体素中心的障碍物遮挡的路径索引组成。系统启动时,路径和邻接列表会被加载到车辆计算机内存中。在线碰撞检查会处理所有感知传感器数据点,并根据邻接表标出相应的闭塞路径。然后,算法遍历每组中的所有路径,根据公式6计算 \(P_B(x_S)\) ,并选择 \(P_B(x_S)\) 最高的路径组。算法返回 \(x_S^*\) 为
\[ x_S^*=\arg \max P_B(x_S) \tag{11} \]
\(n\) 是路径组中的路径数。设 \(h\in\mathbb{Z}^+\) 为路径组的个数,\(m\in\mathbb{Z}^+\) 为感知传感器数据点的个数。在线处理算法如算法1所述
\[ \begin{aligned} \hline \\ &\large{\textbf{算法3}:计算探索路径} \\ \hline \\ &\textbf{输入:} 路径组,邻接列表,\text{2D}的P_B(x_j^k)或\text{3D}的P_B(x_j^{l,k}),i,k,l\in\mathbb{Z} \\ &\textbf{输出:} x_s^*或者没找到路径 \\ &\textbf{begin} \\ &\qquad 初始化所有路径为未碰撞 &//\space\mathcal{O}(nh) \\ &\qquad \textbf{for}\space \text{each} \space 感知到的传感器数据点 \space \textbf{do} &//\space\mathcal{O}(mnh) \\ &\qquad \qquad 使用邻接列表把响应的路径标记为碰撞 &//\space\mathcal{O}(nh) \\ &\qquad \textbf{end} \\ &\qquad \textbf{if}\space 不是所有的路径都碰撞\space \textbf{then} &//\space\mathcal{O}(1) \\ &\qquad \qquad \textbf{for}\space \text{each} \space 路径组 \space \textbf{do} &//\space\mathcal{O}(nh) \\ &\qquad \qquad \qquad 根据公式6计算P_B(x_S) &//\space\mathcal{O}(n) \\ &\qquad \qquad \textbf{end} \\ &\qquad \qquad 找到最大P_B(x_S)的路径组并返回x_S^* &//\space\mathcal{O}(h) \\ &\qquad \textbf{end} \\ &\qquad \textbf{else} \\ &\qquad 返回未找到路径 &//\space\mathcal{O}(1) \\ &\qquad \textbf{end} \\ &\textbf{end} \\ \hline \\ \end{aligned} \]
定理1. 在线处理算法的计算复杂度为 \(\mathcal{O}(mnh)\)
定理1分析了最坏情况下的计算复杂度,即每个感知传感器数据点都会阻塞每组中的所有路径。在实践中,一个数据点可能只阻塞几条路径,因此计算量要小得多。全局范围内的概率传播使用覆盖环境的第二个体素网格,只在导航前运行一次。该算法实现和A*算法有些相似,其中只更新与开放集中相邻体素的概率密度。如果包含 \(A\) 的体素中概率密度的变化小于阈值,则该过程终止。
在没有先验地图的情况下,在公式6中我们也可以使用启发式函数来计算 \(P_B(\xi_i)\):
\[ P_B(\xi_i)=\begin{cases} -|\Delta y_i|, &\text{2D条件},\\ -|\Delta p_i\Delta y_i|, &\text{3D条件}, \tag{12} \\ \end{cases} \]
其中 \(\Delta p_i\) 和 \(\Delta y_i\) 为 \(\xi_i\) 和目标方向的相对的俯仰角和方位角